ответ: x= π/2+2*π*n n∈Z
x=2*π*n n∈Z
Объяснение:
Известно , что : -1<=sinx<=1
-1<=cosx<=1
Решение при котором sinx =-1 , а сosx=0 соответственно и наоборот неподходит : (-1)^5+0^3=-1 или (-1)^3 +0^3=-1
Очевидно , что уравнение имеет тривиальные решения при которых : сosx=1 или sinx=1
Иначе говоря :
x= π/2+2*π*n n∈Z
x=2*π*n n∈Z
Предположим , что существуют нетривиальные решения при которых sinx ≠+-1 и cosx ≠+-1
При возведении в степень большую единицы числа по модулю меньшего единицы оно уменьшается по модулю и cos^2(x) >=0 и sin^2(x)>=0
Таким образом, независимо от того, какой знак имеют sinx и сosx
Cправедливы следующие неравенства
sin^3(x)<sin^2(x)
cos^5(x)<cos^2(x)
Cложим эти неравенства почленно
sin^3(x)+cos^5(x)<sin^2(x)+cos^2(x)=1
sin^3(x)+cos^5(x)<1
То есть мы пришли к противоречию , таких нетривиальных решений не существует.
ответ : x= π/2+2*π*n n∈Z
x=2*π*n n∈Z
Объяснение:
Рисунки к вопросу в приложениях.
Задача 21.11 В какой координатной четверти может находиться угол.
1) |sinα| = sinα - в I и II четвертях окружности.
2) |sinα| > sinα - в III и IV четвертях окружности.
3) |cosα| = cosα - в I и IV четвертях окружности.
4) |cosα| > cosα - во II и III четвертях окружности.
5) |tgα| = tgα - в I и III четвертях окружности.
6) |tgα| > tgα - в II и IV четвертях окружности.
7) |ctgα| = ctgα - в I и IIII четвертях окружности.
8) |ctgα| > ctgα - во II и IV четвертях окружности.
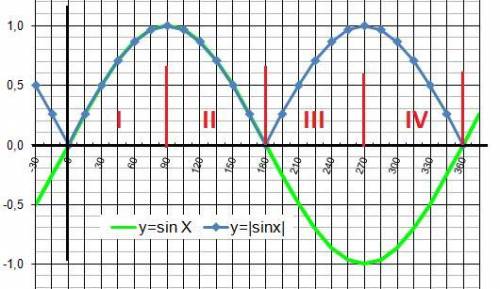
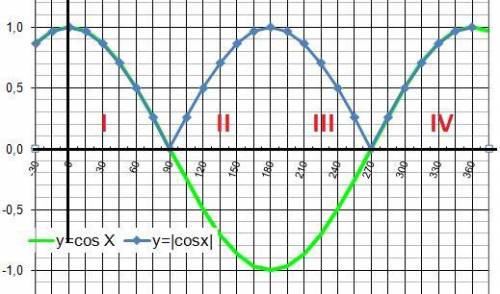
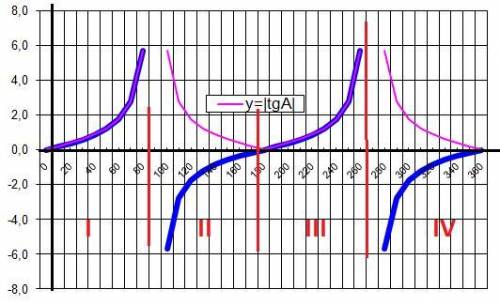
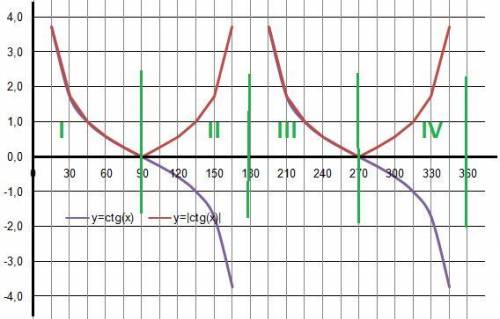
Третья четверть.