Часовая и минутная стрелки догоняют друг друга раз в 65 минут. Если они догоняют друг друга раз в 66 минут, то часы спешат на 1 минуту. Или же, если очень-очень точно считать, то, когда минутная проходит час от часовой, то проходит 60 минут, но минутная впереди на 5 минут. Когда минутная доходит до того 65-отрезка, то часовая еще 5/12 минут... и так очень долго будет продолжаться, пока геометрическая прогрессия не достигнет некоего предела. У меня получилось, что часы спешат на 6/11 минут, но вряд ли тут про это спрашивают). Хотя задача интересная.
Здравствуйте, Sonya2006f!
Чтобы восстановить неполный квадрат суммы, нужно представить крайние члены данной формулы в виде числа со степенью.
Разложение чисел на простые множители:
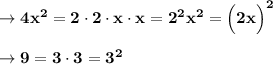
Теперь когда мы знаем, как представить данные члены в виде числа со степенью, запишем формулу, по которой выполнялось разложение.
Формула сокращённого умножения:
НЕПОЛНЫЙ КВАДРАТ СУММЫ: 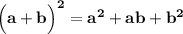 .
.
Зная, что первоначально выражение имело вид  , перемножим по формуле эти члены между собой и получим ответ на Ваш вопрос.
, перемножим по формуле эти члены между собой и получим ответ на Ваш вопрос.
Разложение данного выражения на множители:
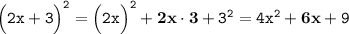
Окончательный ответ данной задачи:
Неполный квадрат суммы данного выражения - "6x".
С Уважением, NeNs07.
Пусть (x₀; y₀) - точка касания. Тогда известно, что касательные проходят через точки (-1; -33) и (x₀: y₀). Составим систему уравнений:
Угловой коэффициент касательной равен значению производной в точке касания
Подставляем
Точка касания лежит на параболе, а значит можно добавить еще одно уравнение.
Осталось составить уравнения касательных
ответ: y=9x-24, y=-23x-56