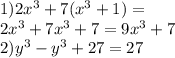
1) 2a^3+7(x^2-x+1)(x+1) =
2a³ + 7x³ +7x² -7x² -7x +7x +7 = 2a³ + 7x³ + 7
2) y^3-(y-3)(y^2+3y+9) = y³ - y³ - 3y² - 9y + 3y² +9y +27 = 27
рассмотрим четырехугольник авсе
1. отрезок вд равен отрезку ед (по условию),
2. отрезок сд равен отрезку ад (вд - медиана),
следовательно, четырехугольник авсе - параллелограмм ( по свойству диагоналей параллелограмма).
значит, прямые вс и ае параллельны.
рассмотрим углы всд и еад: прямая вс параллельна ае ( по свойству параллелограмма), ас - секущая (пересекает обе прямые), значит угол всд = еад = 40 градусов.
угол вае равен сумме углов вад и еад, значит угол вае = 40 + 56 = 96 градусов.
ответ: угол вае равен 96 градусов.
Предположим, что существует какое-либо дробное число, при возведении которого в квадрат можно получить два: (p/q)^2 = 2. При этом эта дробь несократима.
Запишем уравнение так: p^2 / q^2 = 2.
Умножим обе части уравнений на q^2, получим: p^2= 2q^2.
Выражение 2q^2 в любом случае должно быть четным, т. к. выполняется умножение на 2.
Значит, p^2 тоже четно.
Но известно, что квадрат нечетного числа дает нечетное число (например, 5^2 = 25), а квадрат четного – четное (4^2 = 16). Поэтому p должно иметь четное значение.
Если p четно, то его можно представить как p = 2^k. Тогда получим: (2k)^2 = 2q^2. Или 4k^2 = 2q^2.
Сократим полученное уравнение и получим: 2k^2 = q2.
Поскольку в левой части уравнения результат будет четным (т. к. происходит умножение на 2), то и q должно быть четным, чтобы его квадрат был четным.
Но вспомним,
ранее было доказано, что и p четно,изначально предполагалось, что взятая дробь p/q несократима.Если же и p, и q четные числа, то образованную ими дробь можно сократить на 2. Т. е. приходят к противоречию с условием и на этом основании делают вывод, что нет рациональной дроби, квадрат которой может быть равен 2.