пусть пешеход, вышедший из А, после встречи км. Тогда его скорость v1=S/t =
= 3x/2 км/час (40 мин = 2/3 час).
Пешеходу, вышедшему из В, после встречи пришлось пройти x + 2 км. Тогда его скорость
v2=S/t = 2(x+2)/3 км/час (1 час 30 мин = 3/2 час).
До встречи первый затратил время t = (x+2)/v1 = 2 * (x+2)/(3x).
До встречи второй затратил время t = x/v2 = 3 * x/(2(x+2)). Времена затраченные до встречи равны. Составляем уравнение.
(2x + 4)/3x = 3x/(2x+4)
(2x + 4)² = 9x²
либо 2x + 4 = 3x. x=4, либо
2x + 4 = -3x. x=-4/5 (не имеет смысла).
Искомое расстояние S = x + x + 2 = 4 + 4 + 2 = 10 км
Есть и другие упростить данную дробь, однако я предпочитаю этот , так как, на мой взгляд, он довольно простой и самое главное - быстрый.
Наша задача представить слагаемое "2х" в виде суммы/разности двух слагаемых так, чтобы из всех получившихся слагаемых в числителе можно было что-то вынести за скобку.
Таким образом, представим "2х" как разность "3х-x" (так как "3х-х=2х"):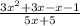
Сразу видно, что можно вынести общий множитель "3x" в числителе у двух слагаемых. Также вынесем общий множитель "5" из выражения в знаменателе.
Необходимо в числителе создать ещё одну скобку, которую мы также вынесем в качестве общего множителя. Заметно, что можно вынести "-1" или просто минус "-" из числителя в части "-х-1", чтобы после вынесения получилось "x+1", которую мы вынесем, как общий множитель.
Сократим общий множитель "x+1", после чего выражение будет упрощено.
ответ: