1.3(−k−e)
2.(−e−k)⋅3
3.(−k−e)⋅3
 , где A, B, C - координаты нормального вектора плоскости N(A,B,C).
, где A, B, C - координаты нормального вектора плоскости N(A,B,C). ⇒ N(2,-3,4).
⇒ N(2,-3,4). , где
, где 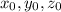 - координаты точки M(
- координаты точки M(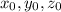 ), через которую проходит прямая,
), через которую проходит прямая,  - координаты направляющего вектора S(
- координаты направляющего вектора S( ).
). ) = N(A,B,C) ⇒ N(2,-3,4) = S(2,-3,4); M(1,-2,3).
) = N(A,B,C) ⇒ N(2,-3,4) = S(2,-3,4); M(1,-2,3).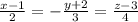
Выражению −3k−3e равны выражения
3(−k−e)
(−e−k)⋅3
(−k−e)⋅3