Четыре последовательных натуральных числа таковы , что произведение двух меньших из них чисел на 78 меньше ,чем произведение больших чисел. Найдите наименьшее из этих чисел.
Решение.
Пусть х - первое число, оно же является наименьшим;
(х+1) - второе число;
(х+2) - третье число;
(х+3) - четвертое число, тогда
х·(х+1) - это произведение двух меньших из данных чисел, а
(х+2)·(х+3) - это произведение двух больших из данных чисел.
По условию
х·(х+1) < (х+2)·(х+3) на 78
получаем уравнение:
(х+2)·(х+3) = х·(х+1) + 78 (ОДЗ; x∈N;)
x²+2x+3x+6 = x²+x+78
4x = 72
x = 72 : 4
x = 18
Получим четыре числа: 18; 19; 20; 21 из них
18 - является наименьшим.
ответ: 18.
Объяснение:
номер 1:
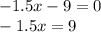
теперь мы освобождаем х, т.е. делим на (-1,5):

ответ: б
номер 2:
y-x=1
y+x=1
уравнения в системах, мы можем складывать, делить, умножать, вычитать, но я хочу сложить:
у+у+х+(-х)=1+1
2у=2|:2
у=1
мы узнали, чему равен у, теперь подставим этот у в одно из уравнений нашей системы, например, в первое:
1-х=1
-х=1-1
-х=0|:(-1)
х=0, и получилось у тебя решение этой системы х = 0, а у = 1 или (0;1)
ответ: в
номер 3:
упростить выражение, в данном случае, раскрыть скобки, найти подобные и посмотреть, что останется:
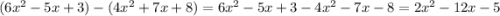
ответ: б