1) Пусть a - длина одной из сторон прямоугольника,
b - длина другой его стороны,
тогда его периметр равен:
2(a+b) = 56
a+ b = 56 : 2
a+b = 28
b = 28-a
2) По тереме Пифагора найдём диагональ данного прямоугольника:
a² + b² = 20²
Подставим вместо b его значение и получим квадратное уравнение:
a² + (28-a)² = 20²
ОДЗ: a<20
a²+784-56a+a²=400
2a²- 56a + 384 = 0
a² - 28a +192 = 0
D = 784 - 4·1·192 = 16 = 4²
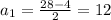
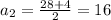
При a₁=12 => b₁=28-12=16
При a₂=16 => b₂=28-16=12
ответ: {12; 16}
1 шаг - переворачиваете дроби, т.е. числитель делаете знаменателем, а знаменатель числителем. или выражаюсь культурным языком, находите обратную дробь к данной, при этом меняете показатель на положительный
2 шаг. возводите степень в степень, при этом перемножаете показатели.
3 шаг. произведение дробей прибираете к рукам, т.е. подгоняете под одну дробную черту произведение знаменателей, а числители перемножаете и записываете в числителе, иными словами, записываете по правилу произведение дробей.
4 шаг. Выделяете отдельно одинаковые буквы, отдельно числа, т.е. обосабливаете их для того, чтобы легче сократить.
5 шаг. Сокращаете дроби.
6 шаг. Любуетесь своей работой.
НО я бы решал легче, сделал бы все показатели положительными, а потом сократил. и уже на третьем шаге отдыхал. Удачи.
Изначально нужно сделать выбор 4 из 16 учеников без учета порядка, так как в конченом итоге они все окажутся в команде.
Теперь рассмотрим пожелания и внесем коррективы в этот выбор.
1) "Хулигана Васю брать точно нельзя"
Это означает, что выбирать мы теперь будем не из 16, а из 15 человек.
2) "Лучший геометр в параллели - Петя - однозначно будет в команде"
Это означает, что нам нужно выбрать не 4, а 3 человек, а также выбирать мы будем не из 15, а из 14 человек.
3) "А близняшек Аню и Таню нельзя разлучать ни в коем случае"
Рассмотрим две ситуации.
Первая ситуация. Аня и Таня попали в команду. Тогда, так как в команде точно есть еще и Петя, в ней осталось всего одно свободное место. Незадействованных учеников осталось 12 и любого из них можно добрать в команду. Таким образом, в этом случае мы имеем 12 вариантов.
Вторая ситуация. Аня и Таня не попали в команду. Тогда, в команде есть три свободных места, которые нужно заполнить, выбирая из оставшихся 12 учеников. Чтобы определить число это сделать, нужно посчитать число сочетаний из 12 по 3:
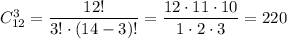
Таким образом, в этом случае мы имеем 220 вариантов.
Но так как первая и вторая ситуация несовместны (Аня и Таня не могут одновременно быть и не быть в команде), то полученные количества вариантов нужно сложить. Итого, число собрать команду:
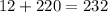
ответ
пусть стороны пр-ка равны а и в,тогда получим систему
{a²+b²=20²,a+b=28
{a=28-b,(28-b)²+b²=400,
784-56b+b²+b²-400=0⇒2b²-56b+384=0,b²-28b+192=0,D1=196-192=4,√D1=2
b1=12,b2=16 ⇒a1=16,a2=12
т.е. стороны пр-ка равны 12 и 16.