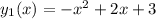 (1)
(1)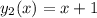 (2)
(2)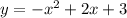 (1)
(1)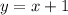 (2)
(2)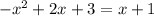
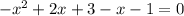
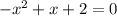 (3)
(3)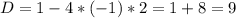
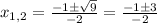
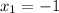
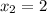
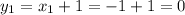
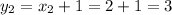
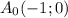

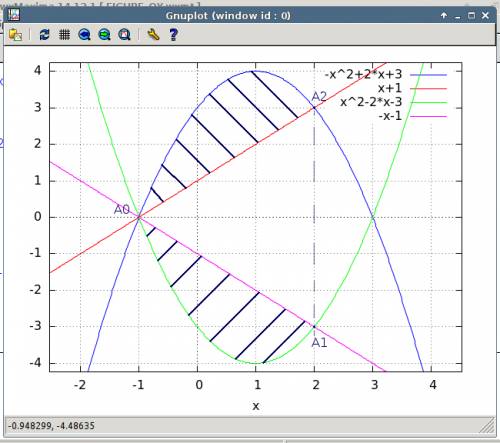
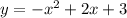 в параболу
в параболу  .
.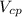 будет равен:
будет равен: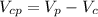 (4)
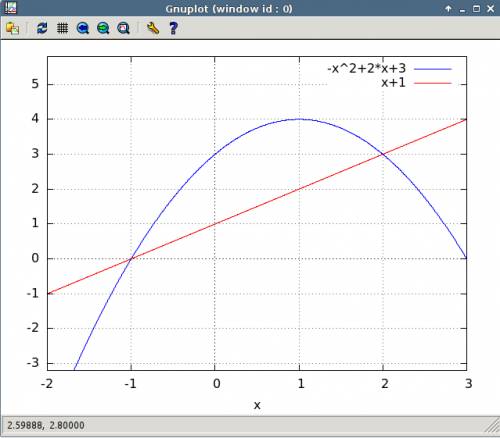
(4)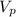 объем фигуры ограниченной, параболами и плоскостью перпендикулярной плоскости рисунка и проходящей через прямую
объем фигуры ограниченной, параболами и плоскостью перпендикулярной плоскости рисунка и проходящей через прямую 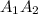 .
.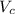 ? , объем конуса ограниченного прямыми и той же плоскостью проходящей через
? , объем конуса ограниченного прямыми и той же плоскостью проходящей через 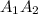
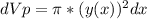
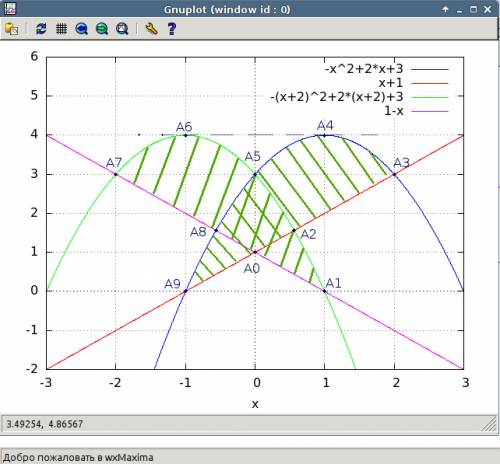
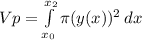 (5)
(5)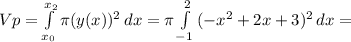
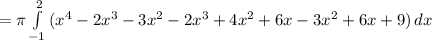
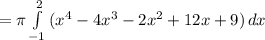 (6)
(6)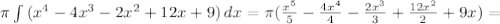
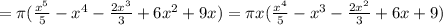 (7)
(7)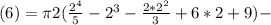
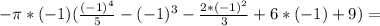
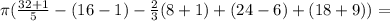
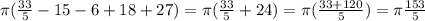 (8)
(8)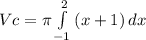 (9)
(9)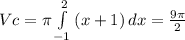 (10)
(10)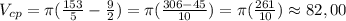
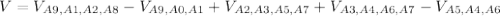
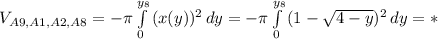
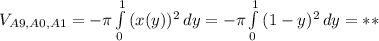

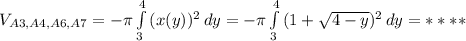

Многочлен стандартного вида - это многочлен, в котором все слагаемые имеют стандартный вид и в котором приведены подобные слагаемые (имеют одинаковую буквенную часть).
Степень многочлена - это степень наибольшего одночлена, в ходящего в многочлен.
1) 22а² - 40а³ + 18а² + 29а³ + а⁴ = а⁴ - 11а³ + 40а²; степень - 4;
2) -7b⁵ - 13b⁶ + 15 - 9b⁵ + 34b⁶ = 21b⁶ - 16b⁵ + 15; степень - 6;
3) 41c² + 62c³ - 99 - 42c² + 38c³ = 100c³ - c² - 99; степень - 3;
4) -52k + k⁴ - 18k⁴ + 52 - k = -17k⁴ - 53k + 52; степень - 4.