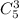Ввазе стоят 10 белых и 5 красных роз. определите, сколькими из вазы можно выбрать из трёх цветов, в котором будет не меньше двух красных роз. как это решить через комбинации?
Не меньше 2-х кр. цветов - это значит, больше или равно 2-м красным цветкам, то есть из выбранных 3-х цветков должно быть либо 2 красных цветка, либо 3 красных цветка.
3) 0 < x ≤ 2 2x+1 ≤ -(x²-2x) 2x+1 ≤ -x²+2x x²+1 ≤ 0 х∈∅, т.к. значение х²+1 неотрицательно при любом х
4) х>2 2x+1 ≤ x²-2x x²-4x-1 ≥ 0 см решение выше в п.2) С учётом того, что x>2, получаем x∈[2+√5; +∞) Объединяя полученные интервалы получаем ответ: x∈(-∞; 2-√5] U [2+√5; +∞)
Всего 10 белых +5 красных цветов.
Не меньше 2-х кр. цветов - это значит, больше или равно 2-м красным цветкам, то есть из выбранных 3-х цветков должно быть либо 2 красных цветка, либо 3 красных цветка.
Выбираем 3 цветка, из них 2 красных и 1 белый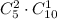
Выбираем 3 цветка и все 3 цветка красные