Объяснение:
Сначала упрощаем предел, в числителе у нас квадратное уравнение, я раскладываю их по таким формулам, т.к теорема виета тут не нужна и дискриминант, потому что корни уравнения нас не интересуют, к тому же, с этими формулами нужно делать меньше действий
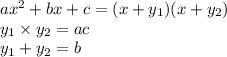
при этом если у нас а>1, bx нужно разложить в виде суммы y1 и y2 и только потом выносить общий множитель
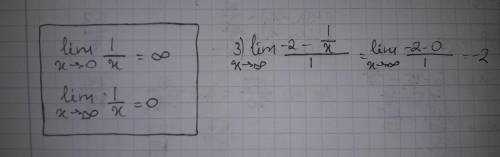
после упрощения, нам нужно просто подставить под х, то значение к которому оно стремится
в последнем пределе я разделила всё на х, потому что бесконечность делить на бесконечность это не очень удобно, чтобы избежать таких ситуаций, можно разделить всё на х, тогда в знаменателе будет бесконечность, и дробь будет равнятся 0

1 2
2 4
3 8
4 16
5 32
6 64
7 128
8 256
9 512
Как видим, последняя цифра меняется так: 2, 4, 8, 6.
А далее эта последовательность повторяется. То есть имеем повторяющуюся последовательность из четырёх цифр.
Чтобы понять, на какую из этих цифр заканчивается 2^2015, мы разделим 2015 на 4. Получим 503 и остаток 3.
Чтобы далее было понятно, рассмотрим варианты:
1) если бы разделилось нацело (как, например, четвёртая степень), то число бы оканчивалось на шесть (смотри выше посчитанные степени)
2) если был бы остаток 1 (как, например, для пятой степени), то число бы оканчивалось на 2
3) если был бы остаток 2 (как, например, для шестой степени), то число бы оканчивалось на 4
4) а если остаток 3 (как, например, для седьмой степени), то число будет оканчиваться на 8
Соответственно, последняя цифра числа 2^2015 будет восемь.