Объяснение:
1) cos²x + 0,1cosx = 0
нужно для удобства вынести cos²x за скобки:
cos²x( 1 + 0,1) = 0
1,1 * cos²x = 0
мы можем просто поделить левую и правую часть на одно и тоже число, например на 1,1 , дабы избавиться от этого бесполезного числа :)
1,1 / 1,1 это 1 ; а 0 / 1,1 это 0:
cos²x = 0 /// с квадратом также
и получаем:
cos x = 0
косинус x равен нулю только в точке:
x= π/2 + πn , где n€ Z
2) sin тут не совсем понятно, объясните в комментариях к этой записи, что именно тут написано sin x или вы хотели sin²x?
1.Область определения D(x) - Х∈(-∞;+∞) - непрерывная. Вертикальных асимптот - нет
2. Пересечение с осью Х. Решаем квадратное уравнение: Y=0
при х1,2 = - 1/3.
3. Пересечение с осью У. У(0) = 1.
4. Поведение на бесконечности.limY(-∞) = + ∞ limY(+∞) = +∞ - горизонтальных асимптот - нет.
5. Исследование на чётность.Y(-x) = 9*x² - 6*x+1 ≠ Y(x).
Функция ни чётная ни нечётная.
6. Производная функции.Y'(x)= 18*x -6 = 0.
Корень Х= -1/3.
7. Локальные экстремумы. Минимум – Ymin(- 1/3) =0.
8. Интервалы возрастания и убывания. Возрастает - Х∈(-1/3;+∞),
убывает = Х∈(-∞;-1/3)
8. Вторая производная - Y"(x) = 18.
Корня производной - точка перегиба - нет.
9. Вогнутая – «ложка» Х∈(-∞;+∞).
10. Область значений Е(у) У∈(0;+∞)
11. Наклонная асимптота -. Уравнение: lim(oo)(k*x+b – f(x).
k=lim(∞)(9x+6+1)= ∞ - наклонных асимптот - нет
12. График в приложении.
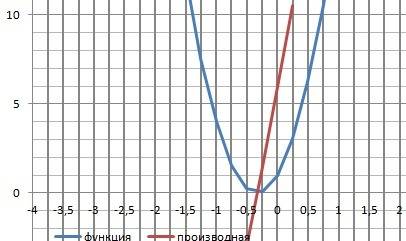
Здравствуйте!
Вот ваше решение: