8
Объяснение:
В конце произведения получим 0, если 5 умножается на чётное число. То есть количество нулей в конце N! зависит от количества 2 и 5 в произведении. Так как в произведении 1•2•3•4•...•37 количество 2 больше чем 5, то достаточно посчитать количество 5:
5, 10=2·5, 15=3·5, 20=4·5, 25=5·5, 30=6·5, 35=7·5 - количество 5 равен 8.
Значит, произведение 1•2•3•4•...•37 оканчивается на 8 нулей.
Количество нулей в конце N! определяется по формуле
![\tt \displaystyle S(N)=\left [\frac{N}{5} \right]+\left [\frac{N}{25} \right]+\left [\frac{N}{125} \right]+...,](/tpl/images/0612/8543/b9dbf.png)
где [a] - целая часть числа a.
Так как 1•2•3•4•...•37=37! и
![\tt \displaystyle \left [\frac{37}{5} \right]=7, \;\left [\frac{37}{25} \right]=1, \; \left [\frac{37}{125} \right]=0,](/tpl/images/0612/8543/77070.png)
то
S(37)=7+1=8.
Это парабола, которая вниз, координаты вершины (1;9), ось симметрии x=1. Найдём точки пересечения с осями: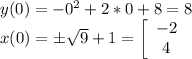
Можем строить график, видим он находится во всех четвертях, но больше всего в 3 и 4.