Зная, что ряд , найти сумма ряда, полученного путем перестановки его членов [tex]1+\frac{1}{3} -\frac{1}{2}+\frac{1}{5} +\frac{1}{7} -\frac{1}{4}+/tex]
АВ/АС = ВЕ/ЕС. Т. к. АВ = ВС то треугольник равнобедренный и высота ВО делит АС пополам. Примем ВО = Х, тогда АВ = 2Х и АО = кв. корень из 3Х ^2, или АО = Х корней из 3. Тогда АС = 2Х корней из 3. Примем ЕС = Y. Можно составить систему уравнений: (ЕС + ВЕ = АВ) т. е. Y + 8 = 2Х 2Х/2Х корней из 3 = 8/Y сократив на 2Х, получим 1/ корень из 3 = 8/Y. Решая систему, находите Y затем Х. Площадь находится перемножением АО на ВО. У меня получилось 32( 3 + 2 корней из 3). Я конечно не уверенна. Торопилась.
АВ/АС = ВЕ/ЕС. Т. к. АВ = ВС то треугольник равнобедренный и высота ВО делит АС пополам. Примем ВО = Х, тогда АВ = 2Х и АО = кв. корень из 3Х ^2, или АО = Х корней из 3. Тогда АС = 2Х корней из 3. Примем ЕС = Y. Можно составить систему уравнений: (ЕС + ВЕ = АВ) т. е. Y + 8 = 2Х 2Х/2Х корней из 3 = 8/Y сократив на 2Х, получим 1/ корень из 3 = 8/Y. Решая систему, находите Y затем Х. Площадь находится перемножением АО на ВО. У меня получилось 32( 3 + 2 корней из 3). Я конечно не уверенна. Торопилась.
Пример
Последовательность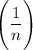 монотонно стремится к нулю, поэтому по признаку Лейбница ряд сходится. Найдем
монотонно стремится к нулю, поэтому по признаку Лейбница ряд сходится. Найдем 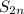
Выпишу формулу Эйлера)))) Пусть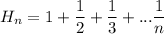 . Эйлер получил асимптотическое выражение для суммы первых n членов ряда:
. Эйлер получил асимптотическое выражение для суммы первых n членов ряда:
где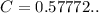 - постоянная Эйлера, при
- постоянная Эйлера, при 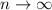 значение
значение 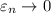
Следовательно,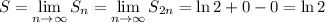
Это мы показали что тот ряд равен ln 2. Теперь перейдем к нашем заданию.
В силу примера, что мы показали в начале, мы получим
Первые две скобки - ряда сходятся, теперь нужно показать что последнее тоже сходится. Рассмотрим ряд
Пусть a > b, тогда
Тут (Sn) - последовательность частичных сумм исследуемого ряда.
Прибавляя и вычитая в выражение слагаемое, мы получим
По формуле Эйлера
Переходя к пределу при n стремящихся к бесконечности, мы получим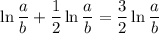
Для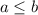 аналогичным образом получается тот же результат. В частности если a = 2, b = 1, получим
аналогичным образом получается тот же результат. В частности если a = 2, b = 1, получим