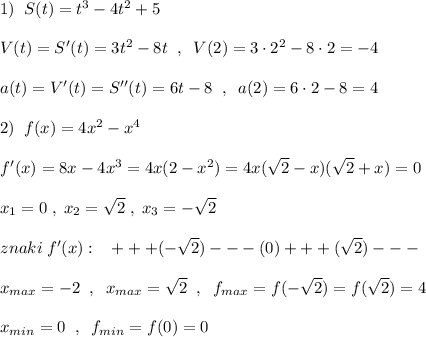
S(t)=t^3-4t^2+5
v(t)=S'(t)=3t^2-8t
a(t)=S''(t)=6t-8
Для момента времени t=2с
v(2)=3×4-8×2=-4
a(2)=6×2-8=4
ответ: v(2) = - 4 ; a(2) = 4 .
Для нахождения экстремумов функции
f(x)=4x^2-x^4 найдем производную.
f'(x)=8x-4x^3
Приравняем к нулю и найденные корни уравнения и дадут нам координаты по Ox точек экстремумов функции.
f'(x)=8x-4x^3=0
4x(2-x^2)=0
4x=0; 2-x^2=0; x^2=2 ;
x1 = 0 ;
x2 = - sqrt2 ;
x3 = sqrt2 ;
В точках
x1 = 0 ;
x2 = - sqrt2 ;
x3 = sqrt2 ;
функция f(x)=4x^2-x^4 имеет свои экстремумы и в этих точках её значения :
y1=f(x1)=0 ;
y2=f(x2)=8-4=4 ;
y3=f(x3)=8-4=4 .
Длина поезда 600 метров.
Объяснение:
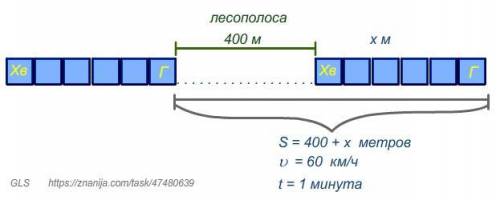
Решим задачу: поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо лесополосы, длина которой 400 м, за одну минуту. Найди длину поезда в метрах.
1) Для начала нужно понять, что значит поезд проезжает мимо лесополосы за одну минуту.
Ориентироваться будем по голове поезда - первому вагону.
Когда первый вагон поравнялся с началом лесополосы, начался отсчет времени движения поезда вдоль лесополосы.
А закончился отсчет времени, когда поравнялись конец лесополосы и конец последнего вагона - хвоста поезда 1 минута.
За это время голова поезда проехала всю лесополосу и еще проехала такое расстояние, чтобы хвост поезда сравнялся с концом лесополосы, то есть голова вперед на длину поезда.
Значит за 1 минуту поезд расстояние, равное длине лесополосы плюс длина поезда.
2) Пусть длина поезда равна x метров. Путь, пройденный поездом равен 400 + x метров.
3) Скорость поезда 60 км/ч, это значит поезд за 1 час (= 60 минут расстояние 60 км, а за 1 минуту он проходит расстояние 1 км.
1 км = 1000 м.
4) За 1 минуту поезд 1000 м, это расстояние равно сумме длины лесополосы и длины поезда.
400 + x = 1000; x = 1000 - 400 = 600 (м).
Длина поезда 600 метров.
найдем координаты векторов АВ и АС, выходящих из вершины А, от координат конца вычтем координаты начала.
→АВ(4-3; 6-5); →АВ(1; 1); →АС(5-3; 5-5); →АВ(2; 0);
найдем длины этих векторов. длина →АВ равна √(1²+1²)=√2; длина →АС равна √(2²+0²)=2;
Найдем скалярное произведение этих же векторов. это сумма произведений соответствующих координат.
→АВ*→АВ=1*2+1*0=2
Разделим скалярное произведение векторов на произведение их модулей, найдя косинус угла между векторами.
2/(2√2)=√2/2, значит. внутренний угол при вершине А равен 45°
ответ 45°