7
Объяснение:
число 7
сумма цифр квадрата предыдущего числа, увеличенного на 1
тут написано увеличенного
предыдущего числа увеличенного на 1 сумма цифр квадрата
тут не написано "сумма цифр квадрата предыдущего числа, увеличенное на 1"
поэтому сначала прибавляем к предыдущему числу 1, находим квадрат и находим сумму цифр
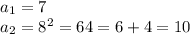
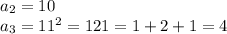
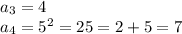
и теперь числа повторяются
каждые 3 раза числа заканчиваются на 4
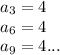
поделим 2011 на 3
оно не делится так как сумма цифр 2+1+1=4 не делится на 3
изменим число 2011 на число поменьше
например 2010 и оно уже делится на 3
поделим
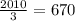то есть оно реально делится, а это значит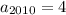 
по логике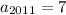 
так как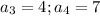 
столько нулей, скока цифр между запятой и первым периодом: 0,11(6) 116-11 105 7 0,11(6)=== 900 900 60 235-2 233 0.2(35)= = 990 990 2) а)Найдем период дроби, т.е. подсчитаем, сколько цифр находится в периодической части. К примеру, это будет число k. б)Найдем значение выражения X · 10k в)Из полученного числа надо вычесть исходное выражение. При этом периодическая часть «сжигается», и остается обычная дробь. г)В полученном уравнении найти X. Все десятичные дроби переводим в обыкновенные. 0,11(6)=Х k=1 10^(k)=1 тогда x*10=10*0,116666...=1,166666... 10X-X=1,166666...-0,116666...=1,16-0,11=1,05 9X=1,05 105 7 X== 900 60 0.2(35): k=2 10^k=100 100X=0.2353535...*100=23,535353 100X-X=23,535353-0.2353535=23,3 99x=23,3 233 x= 900