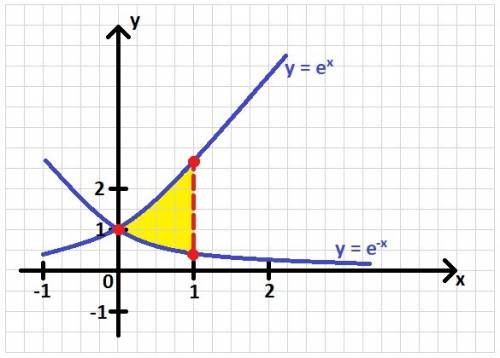
Для решения задачи в первую очередь нужно построить график.
По графику видно, что найти нужно площадь области, лежащей над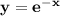 
и под 
.
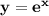Найдём точку пересечения данных кривых. Для этого нужно решить систему из уравнений их функций.
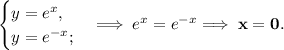
По графику прямая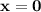 
будет являться границей фигурой слева, а прямая 
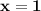— справа.
Найти площадь фигуры, ограниченной сверху графиком функции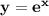 
, а снизу функцией 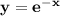, а так же прямым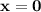и и 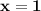, значит вычислить следующий определённый интеграл.
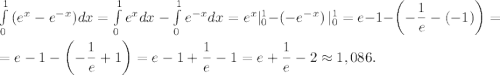
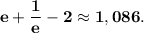
Воспользуемся методом введения вс угла:
1) √2sinx + √6cosx = ...
√(2 + 6) = √8 = 2√2
... = √8(sinx·cos(arccos(1/2) + cosx·sin(arccos(1/2)) = √8sin(x + π/3)
-1 ≤ sin(x + π/3) ≤ 1
-√8 ≤ √8sin(x + π/3) ≤ √8 ⇒ max = √8;
2) 3sinx + 4cosx = 5(sinx·cos(arccos(3/5) + cos·sin(arccos(3/5)) = 5sinx(x + arccos(3/5))
-1 ≤ sinx(x + arccos(3/5)) ≤ 1
-5 ≤ 5sinx(x + arccos(3/5)) ≤ 5 ⇒ max = 5
3) 2siny - 5cosy = √29(siny·cos(arccos(2/√29) + cosy·sin(arccos(5/√29)
max = √29
P.s.: нужно воспользоваться тем, что синус принимает значения на отрезке [-1; 1], а также, что выражение вида Asinx + Bcosy можно привести к виду: