a) x ≥ 3 ; б) x ≥ 5; в) x ∈ [-1; 4]
Объяснение:
1) Так как любое подрадикальное выражение всегда больше или равно нулю, то просто в каждом уравнении на подрадикальное выражение накладываем условие, что оно должно быть больше или равно нулю. Замечу, что в последнем уравнении, нужно найти пересечение x ≥ -1 и x ⩽ 4. В итоге получаем, что x ∈ [-1; 4].
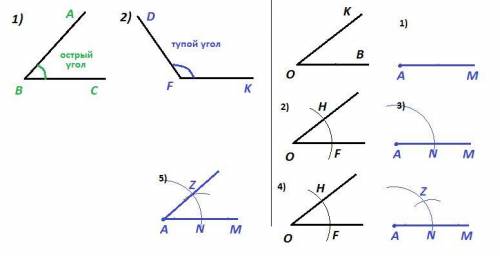
1) Острый угол больше 0° и меньше 90°. ∠ABC
2) Тупой угол больше 90° и меньше 180°. ∠DFK
---------------------------------------------------------
Чтобы построить угол, равный исходному ∠KOB, с циркуля и линейки, нужно :
1) Построить луч AM. Он будет стороной второго угла.
2) На сторонах исходного угла отложить от вершины равные отрезки с циркуля. Отрезки OH = OF
3) На построенном луче циркулем отложить от вершины А точно такой же отрезок и провести дугу. AN = OH = OF
4) В исходном угле измерить циркулем расстояние между засечками FH и отложить его от засечки на луче до пересечения с построенной дугой. NZ = FH
5) Провести луч из вершины A через построенную точку Z. Построенный угол равен исходному ∠NAZ = ∠KOB
a) x>=3
b) x>=2
v) -1<=x<=4
Объяснение: