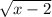Соперник Московского княжества в объединении Русских земель в XV в.

👇

Увидеть ответ

Ответ:

rukisha1107

16.04.2022

Великое княжество Литовское

4,6(19 оценок)

Открыть все ответы

Ответ:

AlinaAlinochka2008

16.04.2022

Достоевский пришел в гости к Гоголю. Позвонил. Ему открыли. "Что вы, - говорят, - Федор Михайлович, Николай Васильевич, уже лет пятьдесят как умер". "Ну, что ж, - подумал Достоевский, царство ему небесное, - я ведь тоже когда-нибудь умру".

***

Однажды Пушкин стрелялся с Гоголем. Пушкин говорит: "Стреляй первый ты. - Как я? Нет, ты! - Ах, я? Нет ты!" Так и не стали стреляться.

***
Однажды Гоголь переоделся Пушкиным, пришел к Пушкину и позвонил. Пушкин открыл ему и кричит: "Смотри-ка, Арина Радионовна, я пришел!"

***

Однажды Гоголь переоделся Пушкиным и пришел к Державину Гавриилу Романовичу. Старик, уверенный, что перед ним и впрямь Пушкин, сходя в гроб, благословил его.

***

Однажды Ф. М. Достоевский, царство ему небесное, исполнилось 150 лет. Он обрадовался и устроил день рождения. Пришли к нему все писатели, только почему-то наголо бритые, как сговорились. Ну, хорошо. Выпили, закусили, поздравили новорожденного, царство ему небесное, сели играть в винт. Сдал Лев Толстой - у каждого по пяти тузов. Что за черт? Так не бывает! Сдай-ка, брат Пушкин, лучше ты! "Я, - говорит сдам!" И сдал всем по шести тузов и по две пиковые дамы. Ну и дела! Сдай-ка ты, брат Гоголь! Гоголь сдал... Ну и знаете... Даже нехорошо сказать. Так как-то получилось. Нет, право слово, лучше не надо.

***

тво ему небесное, гений! Когда же это кончится?". Тут все и кончилось.

4,7(32 оценок)

Ответ:

moskalkov

16.04.2022

5. Посмотрим внимательно на числитель. В нем стоит квадратный трёхчлен относительно $\sqrt{x-2}$ , причем ветви соответствующей параболы направлены вверх. Значит, для всех "больших" иксов числитель положителен. Для того, чтобы неравенство не выполнилось при больших иксах, знаменатель должен быть неположительным. Так как синус от корня при возрастании x принимает все значения от -1 до 1, то 4 - a не может быть больше -1, т.е. a >= 5.
Отметим, что при таком выборе a знаменатель неположителен всегда, а не только при "больших" x, значит, числитель должен быть как минимум неотрицателен (а может, и строго положителен).
Сделаем замену переменной t = sqrt(x - 2), отсюда требование:
t^2 - (a + 4)t + 4a + 1 > 0 при всех t > 0
График функции f(t) = t^2 - (a + 4)t + 4a + 1 - парабола, симметричная относительно прямой t = (a + 4)/2. Так как a >= 5, то наименьшее значение f(t) при t >= 0 принимает в вершине. Для того, чтобы все условия были выполнены, достаточно потребовать
f((a + 4)/2) >= 0
-3 + 2 a - a^2/4 >= 0 (это же неравенство получится, если выделять полный квадрат или выписывать дискриминант)
a^2/4 - 2a + 3 <= 0
2 <= a <= 6
Поскольку a >= 5, то решение - 5 <= a <= 6.
Осталось проверить точку a = 6. Непосредственно подставляя a = 6 в неравенство, получаем, что при t = 5 числитель обращается в ноль, и неравенство из условия выполнено. Стало быть, a = 6 - не решение.
ответ. 5 <= a < 6.

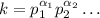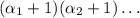6.Несложный комбинаторный факт: если разложение некоторого числа на простые множители имеет вид $k=p_1^{\alpha_1}p_2^{\alpha_2}\dots$ , то у него ровно $(\alpha_1+1)(\alpha_2+1)\dots$ делителей
k делится на 2^2 и 7 и имеет 10 делителей
множитель, связанный с двойкой, не меньше трёх и является делителем 10 -> этот множитель 5 -> 10 = 5 * 2 -> л = 2^(5 - 1) * 7^(2 - 1) = 16 * 7 = 112

4,6(96 оценок)

Это интересно:

12.09.2022

Искусство покорения сердец: как влюбить в себя парня...

Компьютеры-и-электроника

08.07.2020

Как скачать фильм с YouTube через YouTube Downloader...

Компьютеры-и-электроника

25.12.2021

Как правильно отправлять SQL запросы в Mysql из командной строки...

Хобби-и-рукоделие

29.03.2020