Турӑшӑн ӗҫлесси.
Турӑ хӑватлӑ мар, тӳрӗлӗхре.
Турӑ кун парӗ, турӑ апат та парӗ.
Турра юратакансем нумай ырӑлӑх илӗҫ.
Турра шанакан хуйха ӳкмест.
Тӗнчере пурте пирӗн ӑспа мар, Турӑ сучӗпе пулса пырать.
Вӑл ӑна ятлать, Турӑ ӑна сыхлать.
Турӑ айӗнче ҫӳретӗн-Туррӑн ирӗкне ҫӳретӗн.
Турра мӗн кирлӗ, ҫавна тума юрӑхлӑ та.
Турӑ вӑйӗпе хӗрес хурать.
Объяснение:
Жить – Богу служить.
Бог не в силе, а в правде.
Даст Бог день, даст Бог и пищу.
Кто любит Бога, добра получит много.
Тот не унывает, кто на Бога уповает.
Всё в мире творится не нашим умом, а Божьим судом.
Он его бранит, а Бог его хранит.
Под Богом ходишь – Божью волю носишь.
Что Богу угодно, то и пригодно.
Бог по силе крест налагает.
Углы B и C в рассматриваемом равнобедренном треугольнике равны (как углы между основанием и равными рёбрами). Их градусную меру можно определить через известное значение косинуса
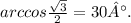
Площадь треугольника найдём как сумму двух одинаковых площадей прямоугольных треугольников. Для этого проведём из вершины A высоту на основание BC. Эта высота AF для равнобедренного треугольника будет также биссектрисой угла A и медианой, делящей основание BC пополам.
Сумма углов треугольника ABC равна 180°. Значит, угол A будет равен 180° - 30° - 30° = 120°. Половина угла равна 60°.
Итак, имеем два равных треугольника ABF и ACF с углами B=C=30° и гипотенузами AB=AC=6. Высоту AF найдём как произведение гипотенузы AB на косинус угла BAF = 0,5 углов A = 60°: AF = 6 · 0,5 = 3. Половину основания найдём из теоремы Пифагора:
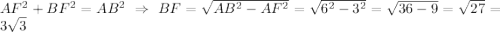
Проверим, зная косинус угла B:
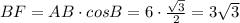
Площадь прямоугольного треугольника равна половине произведения его катетов. Полная площадь равнобедренного треугольника равна сумме площадей равных треугольников ABF и ACF. Получим:
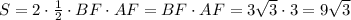
ответы на вопросы
1)1, 3
2)4