Окружностью называется замкнутая плоская кривая, все точки которой равноудалены от заданной точки (центра окружности). Расстояние от любой точки окружности
до ее центра называется радиусом. Центр окружности и сама окружность лежат в одной и той же плоскости. Уравнение окружности радиуса
с центром в начале координат (каноническое уравнение окружности) имеет вид
Эллипсом называется плоская кривая, для каждой точки которой сумма расстояний до двух заданных точек (фокусов эллипса) постоянна. Расстояние между фокусами называется фокусным расстоянием и обозначается через
. Середина отрезка, соединяющего фокусы, называется центром эллипса. У эллипса есть две оси симметрии: первая или фокальная ось, проходящая через фокусы, и перпендикулярная ей вторая ось. Точки пересечения этих осей с эллипсом называются вершинами. Отрезок, соединяющий центр эллипса с вершиной, называется полуосью эллипса. Большая полуось обозначается через
. Эллипс, центр которого находится в начале координат, а полуоси лежат на координатных прямых
Объяснение:
грубо говоря эллипс это растянувшаяся окружность
Теңир тоодогу төрк элдеринин даанышман акыны жана ойчулу Жусуп Баласагындын 1069-1070-ж. Баласагун шаарында жазган саясий-философиялык дастаны. Анын үч көчүрмө нускасы белгилүү. Бири 1439-ж. Герат шаарында (азыркы Түндүк Афганистанда) уйгур жазмасы менен даярдалган (Вена шаарында сакталууда). Экинчиси ХIV к. биринчи жарымында араб жазмасы менен даярдалган Каир нускасы, булардын эң байыркысы - Наманган (Фергана) нускасы ХП к. аягы ХШ к. башында араб жазмасы менен көчүрүлгөн. «Кутадгу билиг». азыр бир катар тилдерге (немец, түрк, орус, өзбек, уйгур, англис, кыргыз ж. б.) которулган. «Кутадгу билигдин» жалпы көлөмү 13444 ыр сабын түзөт, андан тышкары кара сөз түрүндө жазылган чакан кириш сөзү бар, дастанда өлкөнү кантип башкаруу, кантип туура саясат жүргүзүү керектиги айтылат. Ал өтө бай тарыхый-этнографиялык, лингвистикалык, социологиялык ж. б. энциклопедиялык маалыматтарды камтыйт.
111
100
010
000
все легко и просто
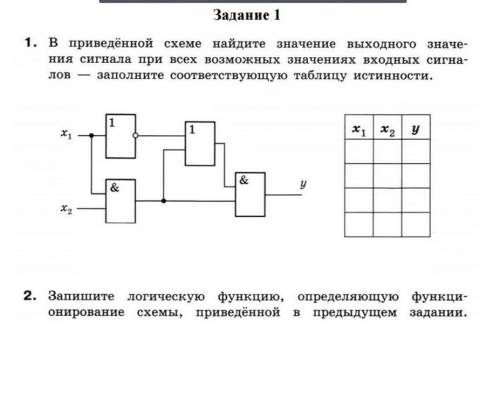
1 ряд-х1
2 х2
3 у