Пошаговое объяснение:
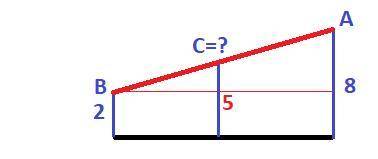
1. Найти середину отрезка.
Рисунок к задаче в приложении.
Три варианта формул:
1) С = (А+В)/2 = (8+2)/5 = 5 - ответ.
2) С = В + (А-В)/2 = 2 + (8-2)/2 = 5 - ответ
3) С = А - (А-В)/2 = 8 - (8-2)2 = = 5 - ответ
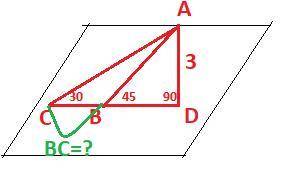
2. Наклонные
Рисунок к задаче в приложении.
Применяем тригонометрические формулы.
AD/BD = tgβ = tg 45° = 1
BD = AD = 3 - отрезок
AD/CD = tg30° = √3/2
AD = 3√3/2 - отрезок
ВС = 3(√3/2 -1) = 3/2*(√3 - 2) - длина отрезка - ответ.
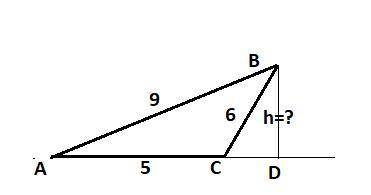
3. расстояние ВМ - равно высоте h(B) треугольника АВС.
Формула для высоты h(B):
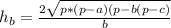
p = (a+b+c)/2 = 10
(p-a) = 4 и (p-b) = 5 и (p-c) = 1
Под корнем = 200
BD = h(b) = 2/5*√200 - высота в треугольнике.
Наклоняем треугольник на 45° и высота становится гипотенузой.
BM = BD*cos45° = 2/5√200*√2/2 = √100/5 = 10/5 = 2 высота - ответ
Физические занятия ценились как необходимая подготовка к войне. Но греки любили спорт и ради него самого, и многие города имели общественный гимнасий (гимнастический зал), где мужчины собирались для физических занятий и отдыха. Они предпочитали индивидуальные состязания командным играм и нередко отмечали религиозные праздники, устраивая в честь богов соревнования по бегу. Именно так впервые начались в 776 г. до н. э. Олимпийские игры. Они проводились каждые четыре года, а их программа расширилась и стала включать прыжки в длину, метание диска и копья, бокс, борьбу, ристание на колесницах и скачки на лошадях, а также поэтические и драматические состязания.