Можно обойтись и без рисунка, но для наглядности он дан.
Заметим, что в равнобедренном треугольнике биссектриса и медиана, проведенные к основанию, совпадают.
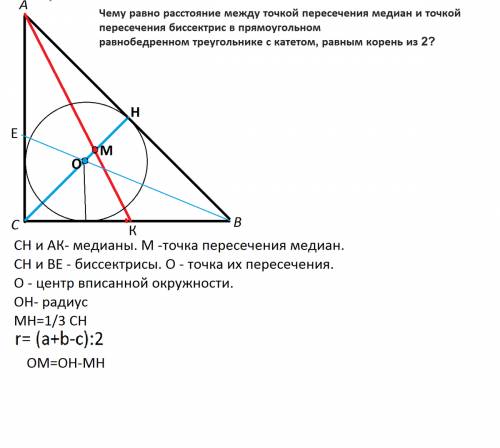
Поэтому СН и АК - медианы и пересекаются с точке М.
Биссектрисы пересекаются в точке О, и эта точка - центр вписанной окружности. Искомое расстояние - ОМ.
В треугольнике АВС гипотенуза
АВ = СВ:sin(45°)=2
CН -медиана и равна половине гипотенузы по свойству медианы прямоугольного треугольника.
СН=1
Медианы треугольника точкой пересечения делятся в отношении 2:1 считая от вершины.
⇒МН- одна треть медианы СН =1/3
ОМ=ОН-МН.
ОН=r= радиус вписанной в АВС окружности.
r=(a+b-c):2= (2√2-2):2=√2-1
ОМ=√2-1-1/3= √2-1¹/₃ = приближенно 0,08088
определим порядок действий: сначала вычисляются результаты отношений в скобках, затем выполняется импликация (поскольку есть «большие» скобки), затем – отрицание (операция «НЕ») для выражения в больших скобках
выполняем операции для всех приведенных возможных ответов (1 обозначает истинное условие, 0 – ложное); сначала определяем результаты сравнения в двух внутренних скобках:
X |
X > 2 |
X > 3 |
(X > 2)→(X > 3) |
((X > 2)→(X > 3)) |
1 |
0 |
0 |
||
2 |
0 |
0 |
||
3 |
1 |
0 |
||
4 |
1 |
1 |
по таблице истинности операции «импликация» находим третий столбец (значение выражения в больших скобках), применив операцию «импликация» к значениям второго и третьего столбцов (в каждой строке):
X |
X > 2 |
X > 3 |
(X > 2)→(X > 3) |
((X > 2)→(X > 3)) |
1 |
0 |
0 |
1 |
|
2 |
0 |
0 |
1 |
|
3 |
1 |
0 |
0 |
|
4 |
1 |
1 |
1 |
значение выражения равно инверсии третьего столбца (меняем 1 на 0 и наоборот):
X |
X > 2 |
X > 3 |
(X > 2)→(X > 3) |
((X > 2)→(X > 3)) |
1 |
0 |
0 |
1 |
0 |
2 |
0 |
0 |
1 |
0 |
3 |
1 |
0 |
0 |
1 |
4 |
1 |
1 |
1 |
0 |
таким образом, ответ – 3.