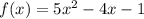
1) Область определения 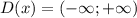
2) Точки пересечения с осями координат
С осью Oy x=0
f(0)=5*0-4*0-1=-1
С осью Ox y=0
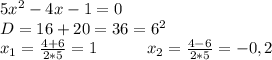
Точки (1; 0) и (-0,2; 0)
3) Четность
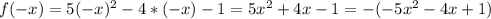
Ни четная ни нечетная
4) Не периодическая
5) Непрерывная
6) 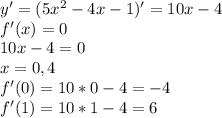
На промежутке 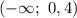 функция убывает на
функция убывает на 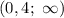 возрастает
возрастает
В точке x=0,4 минимум функции
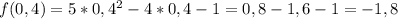
7) 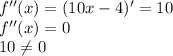
Точек перегиба нет
8) Асимптот нет
9) Построим график функции (во вложении)
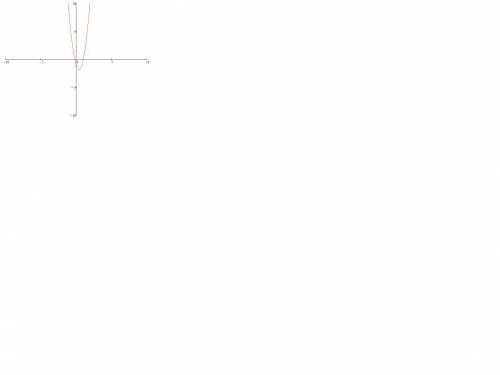
Объяснение:
Синкве́йн (от фр. cinquains, англ. cinquain) — пятистрочная стихотворная форма, возникшая в США в начале XX века под влиянием японской поэзии. В дальнейшем стала использоваться (в последнее время, с 1997 года, и в России) в дидактических целях, как эффективный метод развития образной речи, который позволяет быстро получить результат[1]. Ряд методистов полагает, что синквейны полезны в качестве инструмента для синтезирования сложной информации, в качестве среза оценки пИстория возникновения
В начале XX века форму синквейна разработала американская поэтесса Аделаида Крэпси[en], опиравшаяся на знакомство с японскими силлабическими миниатюрами хайку и танка. Синквейны вошли в её посмертное собрание стихотворений, изданное в 1914 году и несколько раз переиздававшееся.
Правила составления
Традиционный синквейн состоит из пяти строк и основан на подсчёте слогов в каждом стихе: его слоговая структура — 2—4—6—8—2, всего 22 слога (в хайку 17, в танка — 31). Авторы, развивавшие форму в дальнейшем, предложили ряд её вариаций[3]:
Обратный синквейн (Reverse cinquain) — с обратной последовательностью стихов (2—8—6—4—2);
Зеркальный синквейн (Mirror cinquain) — форма из двух пятистрочных строф, где первая — это традиционный, а вторая — обратный синквейны;
Синквейн-бабочка (Butterfly cinquain) — девятистрочная форма со слоговой структурой 2—4—6—8—2—8—6—4—2;
Корона синквейнов (Crown cinquain) — 5 традиционных синквейнов, образующих завершенное стихотворение;
Гирлянда синквейнов (Garland cinquain) — аналог венка сонетов, корона синквейнов, к которой добавлен шестой синквейн, где первая строка взята из первого синквейна, вторая строка из второго, и т. д.
Дидактический синквейн
Дидактический синквейн развился в практике американской школы. В этом жанре текст основывается не на слоговой зависимости, а на содержательной и синтаксической заданности каждой строки.
Первая строка — тема синквейна, заключает в себе одно слово (обычно существительное или местоимение), которое обозначает объект или предмет, о котором пойдет речь.
Вторая строка — два слова (чаще всего прилагательные или причастия), они дают описание признаков и свойств выбранного в синквейне предмета или объекта.
Третья строка — образована тремя глаголами или деепричастиями, описывающими характерные действия объекта.
Четвертая строка — фраза из четырёх слов, выражающая личное отношение автора синквейна к описываемому предмету или объекту.
Пятая строка — одно слово, характеризующее суть предмета или объекта.
Чёткое соблюдение правил написания синквейна не обязательно. Например, для улучшения текста в четвёртой строке можно использовать три или пять слов, а в пятой строке — два слова. Возможны варианты использования и других частей речи.
Синквейн с точки зрения педагогики
Написание синквейна является формой свободного творчества, требующей от автора умения находить в информационном материале наиболее существенные элементы, делать выводы и кратко их формулировать. Помимо использования синквейнов на уроках литературы[4] (например, для подведения итогов по пройденному произведению[5]) практикуется и использование синквейна как заключительного задания по пройденному материалу любой другой дисциплины построения построения синквейна делает его одним из эффективных методов развития ребенка дошкольного возраста, который позволяет быстро получить результат. В частности, знакомство с самим понятием слова и расширение словарного запаса для более эффективного выражения своей мысли[6].
Формирование аналитических Составление синквейна, краткого резюме на основе больших объемов информации, полезно для выработки к анализу. В отличие от школьного сочинения, синквейн требует меньших временных затрат, хотя и имеет более жёсткие рамки по форме изложения, и его написание требует от составителя реализации практически всех его личностных интеллектуальные, творческие, образные). Таким образом, процедура составления синквейна позволяет гармонично сочетать элементы всех трех основных образовательных систем: информационной, деятельностной и личностно ориентированной[7].
Вариативность
Различные вариации для составления синквейна разноплановому составлению заданий. Помимо самостоятельного (как и в паре, в группе) составления нового синквейна, возможны варианты:
составление краткого рассказа по готовому синквейну (с использованием слов и фраз, входящих в состав синквейна);
коррекция и совершенствование готового синквейна;
анализ неполного синквейна для определения отсутствующей части (например, дан синквейн без указания темы — без первой строки, необходимо на основе существующих её определить).онятийного и словарного багажа учащихся[2].
По-перше, не можна заворожено стояти і дивитися на величезну хвилю, як укопаний. Можливо, вам здасться ця рекомендація дивною: кому може прийти в голову стояти і дивитися? Але, як показує практика, багато хто саме так і робить. Чи то від жаху, чи то з цікавості.
По-друге, якщо цунамі вже дуже близько, просто бігти не до тому що хвиля рухається зі швидкістю 800 км на годину (швидкість літака), але чим ближче до берега, тим вона стає повільніше: швидкість знижується до 80 км на годину.
По-третє, якщо цунамі ще далеко, але про нього вже відомо, швидше за все, у вас є не більше 15-20 хвилин для того, щоб втекти. Тому замість того, щоб збирати свої речі, використовуйте час для втечі. Беріть тільки найнеобхідніше. Рятуйте не речі, а життя!
По-четверте, не варто бігти близько русел річок: саме русла річок при цунамі будуть розливатися в першу чергу.
Объяснение:
1) Вершина параболы находиться в точке [0,4;-1,83]
2) Функция убывает [-бесконечности;0,4] (Монотонна на этом промежутке)
3) Функция возрастает [4; +бесонечности] (Монотонна на этом промежутке)
4) Точка экстремума(минимума) совпадает с вершиной параболы.
5) Функция четная.
6) Функция не прерывна на всей области определения
7) Функция ограничена снизу. Прямая ограничивающия функцию y=-1,83
8) Ветви параболы направлены вверх
9)Область определения [-бесконечности;+бесконечности]
10) Область значений [-1,83; +бесконечности]