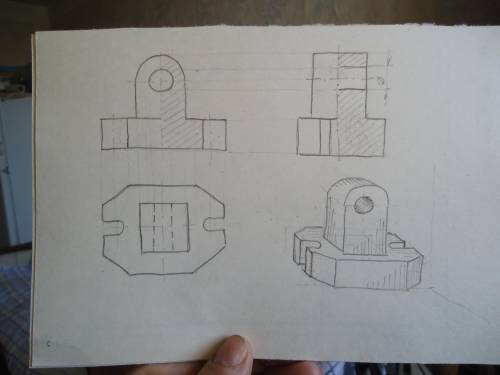
ответ: Чертёж и технический рисунок см. на фото.
Объяснение:
Чертёж построен от руки с сохранением пропорций на глаз для более быстрого ответа. Если нужны на чертеже размеры, проставьте сам.
Разрезы выполнены на виде спереди и виде слева. Я не стала выполнять полный разрез, а выполнила соединение половины вида и половины разреза. В этом случае на половине вида убирают все штриховые линии, а на половине разреза удаляют некоторые видимые линии и штриховые линии выполняют сплошной основной линией.
Для построения технического рисунка, который должен выполняться от руки, я применила построние фронтальной диметрии, чтобы верхние окружности остались также окружностями, и только нижние маленькие окружности имели форму овалов.
При таком построении оси х и z расположены под углом 90°, а ось у расположена под углом 45° к горизонтальной прямой.
По осям х и z размеры откладывают действительные, а по оси у - в два раза меньше. Т.к. это технический рисунок, то пропорции сохраняются на глаз.
Надеюсь, что вам. Желаю успехов.
Задача имеет два способа решения. Первый, который не нравится учителям средней школы, но является наиболее универсальным.
Способ 1.
Применим Теорему Стюарта, согласно которой квадрат медианы равен одной четвертой от суммы удвоенных квадратов сторон из которой вычли квадрат стороны, к которой проведена медиана.
mc2 = ( 2a2 + 2b2 - c2 ) / 4
Соответственно
mc2 = ( 2 * 82 + 2 * 92 - 132) / 4
mc2 = 30,25
mc = 5,5 см
Способ 2.
Второй способ решения, который преподаватели в школе любят - это дополнительные построения треугольника до параллелограмма и решение через теорему о диагоналях параллелограмма.
Продлим стороны треугольника и медиану достроив их до параллелограмма. В этом случае медиана треугольника будет равна половине диагонали получившегося параллелограмма, а две стороны треугольника - его боковым сторонам. Третья сторона треугольника, к которой была проведена медиана, является второй диагональю получившегося параллелограмма.
Согласно теореме, сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его сторон.
2(a2+b2)=d12+d22
Обозначим диагональ параллелограмма, которая образована продолжением медианы исходного треугольника как х, получим:
2( 82 + 92 ) = 132 + x2
290 = 169 + x2
x2 = 290 - 169
x2 = 121
х = 11
Поскольку искомая медиана равна половине диагонали параллелограмма, то величина медианы треугольника составит 11 / 2 = 5,5 см
Ответ: 5,5 см