Пошаговое объяснение:
Перенесём всё в левую часть и выполним необходимые преобразования:
x^2 +x*(m+1-1)+m^2+6(m-1+1)≤0
x^2+xm+m^2+6m≤0
Придавая значения параметру мы получаем квадратное уравнение.
Рассматривать положительные значения параметра мы не будем, потому что так мы не получим отрицательное число.
У нас есть m^2, это самая "опасная" часть нашей "операции".
Найдём значения m, такие чтобы m^2=-6m
m=0;-6;
Значит при (-6;0) в этой части неравенства мы получим отрицательные числа.
Если мы будем брать числа вне этого предела, мы получим слишком большие положительные числа, и решения неравенста не уместяться в наш промежуток: 1<x<2
ответ От -6 до 0 не включая 0
Дано: y = (4- 2x)/(1 -x²),
ИССЛЕДОВАНИЕ.
1. Область определения: D(y)= X≠ ±1 , X∈(-∞;-1)∪(-1;1)∪(1;+∞).
Не допускаем деления на 0 в знаменателе.
2. Разрыв II-го рода при Х = ±1. Две вертикальных асимптоты:
Х = -1, Х = 1.
3. Наклонная асимптота: y = k*x + b.
k = lim(+∞)Y(x)/x = (x/x³) = 0
b = lim(+∞)Y(x) - k*x = 0
Горизонтальная асимптота: y= 0.
4. Пересечение с осями.
С осью ОХ. 4 - 2*x = 0 . Нуль функции: x = 2
С осью ОУ: y(0) = 4.
5. Интервалы знакопостоянства.
Отрицательна: Y(x)<0 - X∈(-∞;-1)∪(1;2).
Положительна: Y>0 - X∈(-1;1)∪(2;+∞;)
6. Проверка на чётность. Есть сдвиг по оси ОХ - нет симметрии ни осевой ни центральной.
Функция общего фида - ни чётная, ни нечётная: Y(-x) ≠ -Y(x) ,
Y(-x)≠ Y(x).
7. Поиск экстремумов по первой производной.
y'(x) = -2/(x-1) + 2/x(4-2*ч)/(x-1)².
x1 = 0,267, x2 = 3,732 - точки экстремумов.
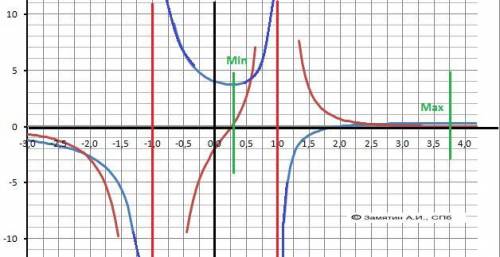
8. Локальный максимум: y(3,73) = 0,27
минимум: y(0,2672) = 3,73.
9. Интервалы монотонности.
Возрастает - X∈(0,267;1)∪(1;+∞). Убывает: X∈(-∞;-1)∪(-1;0,267).
10. Поиск перегибов по второй производной.
y"(x) = (-4*x³+24*x²-12*x+8)/(1-x²)³ = 0.
Точки перегиба, при Х = ± 1 (разрывы) и х=5,52.
11. Вогнутая - "ложка"- X∈(-1;1), выпуклая - "горка" - X∈(-∞;-1)∪(1;+∞)
12. Область значений. E(y) - y∈(-∞;+∞).
13. График функции на рисунке в приложении.