Question

Овремя выполнения лабораторных работ по студенты азат и нияз собрали систему из рычага и блоков, изображённую на рисунке. система находится в равновесии. точки подвеса делят рычаг в отношении а : b = 3 : 2. найдите отношение масс грузов ma : mb, пренебрегая массами рычага, блоков и верёвок, а также трением.

Answer 1

Объяснение: ВНИМАНИЕ! За l2 и F2 я взял отрезок b, а за l1 и F1 я взял отрезок a.

В этой задаче мы будем пользоваться условием равновесия рычага(пропорцией):

$\frac{F1}{F2} = \frac{l2}{l1}$

Эта задача действительно пугает: плечи сил нам неизвестны, вместо них нам дано отношение. Обе силы, с которыми действуют эти грузы, мы не знаем.

Но не все так сложно.

Сначала поговорим о плечах этих сил.

Плечи этих сил можно обозначить любой буквой(будь то буква a, x, d и т.д.)

Я возьму букву x.

Тогда получается, что второе плечо силы равняется 2a см, а первое - 3a см.

Введем эти данные в пропорцию:

$\frac{F1}{F2} = \frac{2a}{3a}$

Но тут у нас появляется счастье в виде двух неизвестных величин F1 и F2. Можно было бы составить систему линейных уравнений и поломать себе жизнь окончательно, но систему мы составлять не будем, все гораздо проще.

Давай мы из этой пропорции выразим F2:

F2 =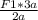 $\frac{F1 * 3a}{2a}$

И тут мы с радостью обнаруживаем, что наше пресловутое a сокращается, и остается 3/2F1, а 3/2 это ничто иное, как 1,5F1

А это значит, что сила F2 в полтора раза больше силы F1.

Теперь мы знаем все. Запишем наши достояния человечества в пропорцию. (Вместо F2 я запишу 1,5F1).

$\frac{F1}{1,5F1} = \frac{2}{3}$

И тут мы с радостью обнаруживаем,что в левой части пропорции сокращается F1, в числителе вместо F1 остается 1(по свойству дроби).

Получаем достояние человечества:

$\frac{1}{1,5} = \frac{2}{3}$

Теперь мы найдем отношение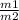 $\frac{m1}{m2}$

1 Н делим на 10 Н/кг получаем 0,1 кг - масса груза a

1,5 Н делим на 10 Н/кг получаем 0,15 кг - масса груза b.

Теперь мы находим отношение двух масс:

$\frac{0,1}{0,15}$ ≈ 0,66

Задача решена.