Если шайба на вершине горки будет иметь относительно земли такую же горизонтальную скорость, как и горка, т.е. если шайба на вершине замрёт относительно горки, то при соскальзывании вправо, за счёт потенциальной энергии, она бы набрала дополнительную скорость относительно горки, так что её скорость относительно земли оказалась бы больше скорости горки .
Аналогично, если бы скорость шайбы на вершине горки относительно земли была бы больше скорости горки, то при соскальзывании вправо, шайба набрала бы относительно земли ещё большую скорость .
Так что понятно, что шайба соскользнёт с горки влево, и равенство скоростей будет выполняться только по модулю, так что совершенно ясно, что:
;
;
;
;
Теперь, по закону сохранения импульса:
;
;
;
Далее, по закону сохранения энергии (умножая сразу же на 2):
;
;
;
;
;
;
;
;
;
Наибольшее приращение потенциальной энергии происходит в тот момент времени , когда горка и шайба движутся, как единое целое, при этом по закону сохранения импульса:
;
Начальная кинетическая энергия шайбы:
;
Минимальная кинетическая энергия совместного движения шайбы и горки в момент наивысшего подъёма:
;
Максимальное приращение потенциальной энергии шайбы в момент наивысшего подъёма:
;
Доля максимального приращения потенциальной энергии от начальной кинетической составляет:
Дано: a - 2,5 см b - 1,2 см c - 65 мм ρ кирпича - 1800 кг/м^3 g - 10 Н/кг Найти: V, m, F Решение: Сначала переведем см и мм в СИ в метры. 2,5 см=0,25 м 1,2 см=0,12 м 65 мм=6,5 см=0,65 м. Теперь найдём объем кирпича по формуле: V=abc Получаем: 0,25*0,12*0,65=0,0195 м^3. Второй шаг. Находим массу тела по его плотности и объему: m=ρV Получаем: 1800*0,0195=35,1 кг. Третий шаг. Найдём силу тяжести, действующую на данный кусок кирпича. В формуле для нахождения силы тяжести используется масса тела и ускорение свободного падения, равное 10 Н/кг - константа. Обозначается буквой g. F=gm Получаем: 10*35,1=351 Н. ответ: на кирпич массой 35,1 кг и объемом 0,0195 м^3 действует сила тяжести, равная 351 Н.
В средние века не было ясного представления о работе и измерении ее. Зато отношение между выигрышем в силе и потерей в скорости было известно. На него и указывали вдумчивые инженеры и исследователи. Знаменитый основатель механики Галилео Галилей также не мимо загадки выигрыша в силе. Еще в юности он написал небольшое сочинение о простых машинах. В нем он убедительно доказывал, что рычаг, подвижный блок и вообще машины, выигрывая в силе, теряют в скорости, то есть не дают выигрыша в работе. Но рядовые техники средневековья еще предавались бесплодным размышлениям о причине выигрыша в силе. Подобно древним, они были уверены, что, пользуясь машинами, им удается «обмануть природу» . Это заблуждение толкнуло изобретателей на ложный путь, когда перед ними возникла задача отыскать удобный и дешевый двигатель.
Объяснение:
Если шайба на вершине горки будет иметь относительно земли такую же горизонтальную скорость, как и горка, т.е. если шайба на вершине замрёт относительно горки, то при соскальзывании вправо, за счёт потенциальной энергии, она бы набрала дополнительную скорость относительно горки, так что её скорость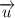 относительно земли оказалась бы больше скорости горки
относительно земли оказалась бы больше скорости горки 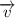 .
.
Аналогично, если бы скорость шайбы на вершине горки относительно земли была бы больше скорости горки, то при соскальзывании вправо, шайба набрала бы относительно земли ещё большую скорость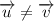 .
.
Так что понятно, что шайба соскользнёт с горки влево, и равенство скоростей будет выполняться только по модулю, так что совершенно ясно, что:
Теперь, по закону сохранения импульса:
Далее, по закону сохранения энергии (умножая сразу же на 2):
Наибольшее приращение потенциальной энергии происходит в тот момент времени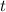 , когда горка и шайба движутся, как единое целое, при этом по закону сохранения импульса:
, когда горка и шайба движутся, как единое целое, при этом по закону сохранения импульса:
Начальная кинетическая энергия шайбы:
Минимальная кинетическая энергия совместного движения шайбы и горки в момент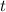 наивысшего подъёма:
наивысшего подъёма:
Максимальное приращение потенциальной энергии шайбы в момент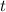 наивысшего подъёма:
наивысшего подъёма:
Доля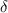 максимального приращения потенциальной энергии от начальной кинетической составляет:
максимального приращения потенциальной энергии от начальной кинетической составляет: