Для начала вспомним формулу кинетической энергии:
Е=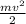
(1) Представим, что мы бросаем этот мяч. Он летит, потом "останавливается" где-то в высшей точке, а потом уже летит вниз. Логично, что если он "останавливается", т.е. не двигается, то и скорость его = 0, следует, по формуле, что кинетическая = 0. ответ 3 верный.
(2) У мяча, пока он летит, скорость не постоянна, иначе как бы он остановился, (так-то еще существуют формулы для свободного падения), значит, что в какой-то момент скорость была наибольшей, а затем начала уменьшаться. Понятно, что скорость максимальна в момент броска. Значит, по формуле кинетическая будет тоже максимальна. ответ 1 неверный.
Неправильность остальных ответов можно объяснить следствиями (2).
Масса автомобиля: т =
т = 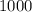 кг.
кг.
Начальная скорость автомобиля: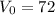 км/ч =
км/ч = 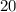 м/с.
м/с.
Конечная скорость автомобиля: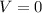 м/с.
м/с.
Так как автомобиль остановится.
Коэффициент трения: .
.
Найти нужно тормозной путь: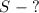
Решение:0. Строим рисунок для упрощения определения направлений сил.
1. Распишем второй закон Ньютона по оси Оy: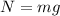 .
.
2. Распишем второй закон Ньютона по оси Ох: .
.
3. Сила трения по определению:
4. Объединим (1) и (3):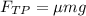 .
.
5. Объединим (2) и (4): .
.
6. Скорость при равнозамедленном движении: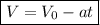
С учётом того, что конечная скорость равна нулю, получим: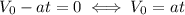 .
.
7. Объединяем (5) и (6):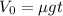 .
.
8. Выразим время из (7): .
.
9. Тормозной путь: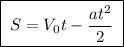
10. Объединяем (5), (8) и (9):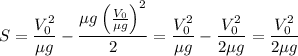 .
.
Численно получим: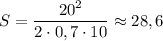 (м).
(м).
ответ: 28,6 м.Более простой по закону сохранения энергии.