Точка участвует одновременно в двух взаимно перпендикулярных гармонические колебаниях, выражаемых уравнениями x=a1 sin ω1t и y=a2 cos ω2t, где a1=8 см, a2=4 см, а циклические частоты ω1= 4с^-1, ω2= 2с^-1. написать уравнение траектории и построить её. показать направление движения точки.

👇

Открыть все ответы

Ответ:

mischad

11.09.2022

Запишем второй закон Ньютона в проекции на ось, направленную вниз вдоль плоскости (Ось x), и на ось, которая сонаправлена скорости тела в любой момент времени. Пусть угол между скоростью тела и горизонталью в произвольный момент времени составляет β', тогда

$\displaystyle m\frac{\Delta v_x}{\Delta t} = mg\sin\alpha - \mu m g\cos\alpha\sin\beta'\\\\m\frac{\Delta v}{\Delta t} = mg\sin\alpha\sin\beta' - \mu m g\cos\alpha$

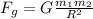
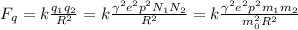
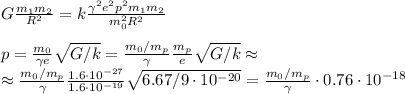
Учтите, что здесь угол бета-штрих - это функция от времени, но никак не постоянная величина. В начальный момент бета-штрих равен 30 градусов. Здесь уже сразу используется выражение для силы трения скольжения на наклонной плоскости (мю эм же косинус альфа) и корректно учтены проекции. Условие задачи и параметры подобраны так, что μ равен тангенсу угла наклона плоскости, и это надо использовать, иначе решать задачу будет в разы сложнее. Итак, имеем

$\displaystyle m\frac{\Delta v_x}{\Delta t} = mg\sin\alpha(1-\sin\beta')\\\\ m\frac{\Delta v}{\Delta t} = mg\sin\alpha(\sin\beta' - 1) = -\displaystyle m\frac{\Delta v_x}{\Delta t}\\\\\Delta v = -\Delta v_x$

Итак, мы получили важное соотношение для приращения проекции скорости и полной скорости. Теперь подумаем. В начале полная скорость была равна v0 (ее надо найти), а в конце станет v. Проекция на ось x в начальный момент равна v0 sinβ, а в конце будет тоже v, так как очевидно, что после большого промежутка времени скорость поперек плоскости гасится трением и остается только скорость вдоль плоскости. Поэтому, суммируя все приращения скорости мы получим

$\displaystyle \Delta v = -\Delta v_x\\ (v-v_0) = -(v-v_0\sin\beta)\\ v_0 = \frac{2v}{1+\sin\beta} = \frac{4v}{3} = 4 (m/s)$

4,4(74 оценок)

Ответ:

Salahaddin001

11.09.2022

Будем считать, что, теряя все электроны, один атом звездного вещества приобретает положительный заряд γe, где e - заряд электрона, γ - некое усредненное количество электронов у одного атома звездного вещества. Звезды состоят из нескольких химических элементов, и приписать γ какое-то конкретное значение возможно, только зная химический состав звезды.

Сила гравитационного взаимодействия звезд

$F_g =G\frac{m_1m_2}{R^2}$

Сила же кулоновского взаимодействия двух звезд с потерянными электронами равна

$F_q = k\frac{q_1q_2}{R^2} = k\frac{\gamma^2e^2p^2N_1N_2}{R^2} = 
k\frac{\gamma^2e^2p^2m_1m_2}{m_0^2R^2}$

Где N1, N2 - числа атомов в звездах, m0 - некая средняя масса одного атома звездного вещества, a p - доля от полного числа N атомов, которые потеряли электроны. Приравняем:

$G\frac{m_1m_2}{R^2} = k\frac{\gamma^2e^2p^2m_1m_2}{m_0^2R^2}\\\\
p = \frac{m_0}{\gamma e}\sqrt{G/k} = \frac{m_0/m_p}{\gamma}\frac{m_p}{e}\sqrt{G/k}\approx\\
\approx\frac{m_0/m_p}{\gamma}\frac{1.6\cdot10^{-27}}{1.6\cdot10^{-19}}\sqrt{6.67/9\cdot10^{-20}} = \frac{m_0/m_p}{\gamma}\cdot0.76\cdot10^{-18}$

Итак, мы записали ответ в достаточно удобной форме. Доля атомов должна быть по порядку величины равна 0.76*10^(-18). Чтобы получить точное значение, надо умножить это число на среднюю массу атома звездного вещества (выраженную в а.е.м, то есть, в массах протона) и разделить на среднее количество электронов в атоме звездного вещества

Для водородно-гелиевых звезд средняя масса атома заключена между 1 и 4, среднее количество электронов - между 1 и 2

4,6(67 оценок)

Это интересно:

Кулинария-и-гостеприимство

23.04.2021

Освежающий и полезный напиток: лимонад из лаймов и имбиря...

Здоровье

23.09.2021

Как сохранить здоровые и крепкие зубы...

Финансы-и-бизнес

09.05.2023

Как эффективно организовать сбор средств для благотворительных целей?...

Компьютеры-и-электроника