Предположим, что шар сплошной.
Тогда масса шара:
m = P/g = 36,9 : 10 = 3,69 (кг)
Объем шара:
V = m/ρ = 3,690 : 8900 ≈ 4,15·10⁻⁴ (м³)
Выталкивающая сила, действующая на шар при его полном погружении, равна весу воды в объеме этого шара:
F(a) = ρ(в)gV = 1000 · 10 · 4,15·10⁻⁴ = 4,15 (H)
Таким образом, если бы шар был сплошным, то его вес в воде при полном погружении составил бы:
P' = P - F(a) = 36,9 - 4,15 = 32,75 (H)
Очевидно, что полученное значение не совпадает с данным. Значит, наше предположение было неверным и в шаре существует полость. Попробуем найти объем этой полости:
Разница в весе шара в воде без полости и с полостью:
P' = F(a)' = 32,75 - 26,7 = 6,05 (H)
Такая разница в выталкивающей силе появится при увеличении объема шара на:
V' = F(a)'/ρ(в)g = 6,05 : 10000 = 6,05·10⁻⁴ (м³)
Объем сплошного медного шара с таким весом в воздухе, как мы выяснили:
V = 4,15·10⁻⁴ (м³)
Разница объемов и будет приходиться на полость внутри шара:
V(п) = V' - V = 6,05·10⁻⁴ - 4,15·10⁻⁴ = 1,9·10⁻⁴ (м³) = 190 см³
ответ: в медном шаре существует полость объемом 190 см³.
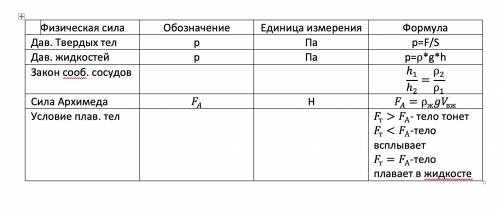
Физическая сила Обозначение Единица измерения Формула
Дав. Твердых тел p Па p=F/S
Дав. жидкостей p Па p=ρ*g*h
Закон сооб. сосудов h_1/h_2 =ρ_2/ρ_1
Сила Архимеда F_A Н F_A=ρ_ж gV_вж
Условие плав. тел F_т 〖>F〗_А- тело тонет
F_т 〖<F〗_А-тело всплывает
F_т 〖=F〗_А-тело плавает в жидкосте
M = 29·10⁻³ кг/моль
Объяснение:
Дано:
m₁ = 0,231·m
M₁ = 32·10⁻³ кг/моль
m₂ = 0,756·m
M₂ = 28·10⁻³ кг/моль
m₃ = 0,013·m
M₃ = 40·10⁻³ кг/моль
M - ?
По формуле:
M = (m₁+m₂+m₃) / ( m₁/M₁ + m₂/M₂ + m₃/M₃)
M = m / ( 0,231·m/M₁ + 0,756·m/M₂ + 0,013·m/M₃)
M = 1 / ( 0,231 / 32·10⁻³ + 0,756 / 28·10⁻³ + 0,013/40·10⁻³)
M = 1 / (7,22 + 27 + 0,33) ≈ 29·10⁻³ кг/моль
Мы действительно получили молярную массу воздуха.