Объяснение:
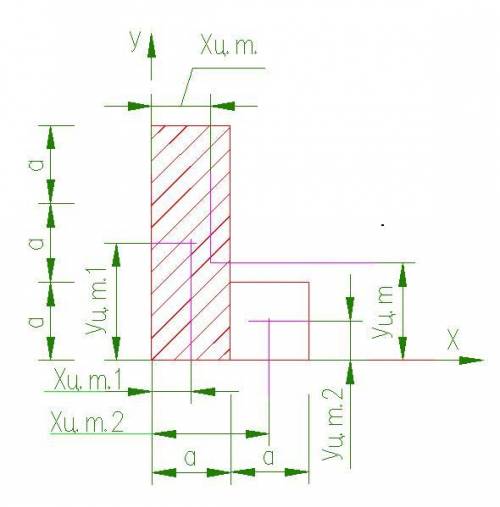
Пластина делится на две прямоугольные части.
У прямоугольника центр тяжести в середине.
У первой - заштрихованной пластины площадь 3a^2
А расстояния от координатных осей до центра тяжести:
Хцт1=0,5а
Уцт1=1,5а
У второй пластины площадь a^2
расстояния от координатных осей до центра тяжести:
Хцт2=1,5а
Уцт1=0,5а
Центр тяжести можно найти если просуммировать площади умноженные на расстояние до центра тяжести каждой простой фигуры, а потом эту сумму поделить на общую площадь.
Общая площадь фигуры 4а^2
Остается посчитать
Хц.т.=(3a^2*0,5а+a^2*1,5а)/4а^2=3а^3/4а^2=3а/4=0,75а
Уц.т.=(3a^2*1,5а+a^2*0,5а)/4а^2=3а^3/4а^2=5а/4=1,25а
Картинка приложена
M(a)g/S=M (p) g/S
тут M(a) и M(p) - массы брусков соотв-но алюминиевого и парафинового.
M(a) = V(a)*P(a) тут V(a) - объём алюминия, а P(a) его плотность, дальше всё точно также
V(a) = h(a)*S
V(p) = h(p)*S
M(p) = h(p)*S*P(p)
M(a) = h(a)*S*P(a)
подставляем в уравнение давления и заменяем известные величины числами из условия.
h(a)*P(a) = h(p)*P(p)
h(a) = 4см = 0.04 м по условию
P(a) = 2700кг/м:3
P(p) = 900кг/м^3
это плотности, их всегда дают в условии, но вы почему - то жадничаете.
дальше получим, что
h(p) = (h(a)*P(a))/P(p) =
P.S. моя жизнь слишком коротка чтобы решать эти задачи для даунов.
ответ: высота парафинового бруска равна 0.12 метрам или 12 сантиметрам.