Дано:
L=200м
l=100м
Найти:
Δr-?
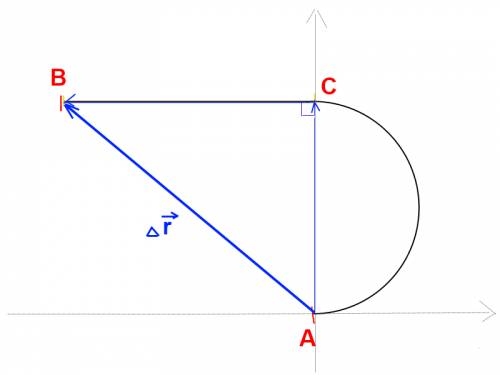
Рисуем схему (см. вложение).
Вектор АВ=АС(вектор)+СВ(вектор)
Т.к. "спортсмен пробегает дистанцию L=200м. Беговая дорожка представляет собой полуокнужность,за которой следует прямолинейный участок длиной l = 100 м", то дуга АС=100м (200м-100м)
Длина окружности (С) равна двум дугам АС
С=200м
АС = диаметру окружности.
С=2πR
С=Dπ
D=C/π
D≈(200/3,14)м≈63,7м
СВ=l=100м
Т.к. векторы перемещения составляют прямоугольный треугольник, модуль вектора перемещения можно найти по теореме пифагора.
Δr²=АС²+СВ²
Δr²=(4057+10000)м
Δr ≈ 119м
ответ: Δr=119м
ДАНО:
H - высота
h - последние 30 метров
V - скорость падения на последних 30-ти метрах.
t = 0,5 с
НАЙТИ:
H
h=Vt+gt*t/2; V=h/t-gt/2
Начальная скорость прохождения участка h равна конечной скорости прохождения предыдущего участка полёта.
H-h=(V*V-V0*V0)/2g; так как тело падает свободно, значит V0=0;
H-h=V*V/2g; подставляем V, получаем такое уравнение:
H-h=h*h/2g*t*t-h/2+g*t*t/8; далее
H=h+h*h/2g*t*t-h/2+g*t*t/8=h/2+h*h/2g*t*t+g*t*t/8=15+180+0,3125=195,3125(м)
ответ: тело упало с высоты 195,3125 метров
m=po*V, за табличними даними ро=0,09кг/м^3.
Звідси m= 0,09*1=0,09кг