Разделим путь полета тела на разные промежутки.
Пусть до последних четырех секунд тело пролетело S₁ м, за предпоследние две секунды тело пролетело S₂ м, а за последние две секунды S₃ м.
Рассмотрим конкретно участки S₂ и S₃.
Время t₂ = t₃ = 2 с ;
Ускорение g = 10 м/с² ;
Начальные скорости v₀₂ и v₀₃ разные. Найдем v₀₂, то есть скорость падения в момент начала пути S₂.
Мы знаем, что S₃ = 2S₂.
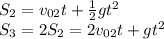
Найдем сумму этих путей, понимая, что сумма этих путей это S₂₃, где
t = 4 с ; g = 10 м/с^2 ; v₀ = v₀₂ ; 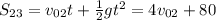
и одновременно подставим все данные значения:
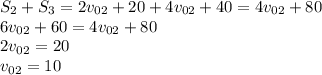
S₂ = 20 + 20 = 40 м
S₃ = 2S₂ = 80 м
Мы знаем, что путь S₁ тело пролетело с ускорением g и набрало скорость от v₀₁ = 5 до v₀₂ = 10 м/с.
По формуле:
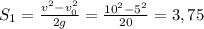
S₁ = 3,75 м
Время за первую часть полёта:
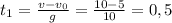
t₁ = 0,5 с
Общий путь (высота, с которой сбросили тело):
h = S = S₁ + S₂ + S₃ = 3,75 м + 40 м + 80 м = 123,75 м
Общее время (время падения):
t = t₁ + t₂ + t₃ = 0,5 с + 2 с + 2 с = 4,5 с
1) h = 123,75 м
2) t = 4,5 с
Так как центр движется с ускорением g, то он неподвижен и вращение осуществляется относительно него
Скорость точек будет векторно складываться из скорости в плоскости вращения и скорости падения. Модуль вектора скорости падения в момент t равен ; Линейная скорость при движении по окружности связана с угловой соотношением
Результирующие вектора скоростей A и B - это две различные диагонали соответствующих параллелограммов, которые они образуют при сложении векторов.
Угол α, между горизонтом и стержнем, равен по условию t*w=(2/6)pi = pi/3=60°; Значит тупой угол параллелограмма равен 90°+30°=120°.
По теореме косинусов: ; Учитывая, что R=L/2 и упрощая, получаем: (приняли, что g=10);
Для второй точки: ;
Упрощая: