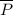Поїзд, який рухався зі швидкістю 36км/год, почав гальмувати з прискоренням 0,8м/с². Визначте швидкисть поїзда через 10хв після початку гальмування?

👇

Увидеть ответ

Открыть все ответы

Ответ:

urkashkz777

27.04.2021

Объяснение:

Буду считать то что опыты ( по определению массы ) провожу с не упругим материалом заранее зная его плотность

Поставить тело электронные весы и определитить массу

Для начала можно измерить объём шарика как минимум

1) по формуле

V = ¾πR³

( радиус шарика можно измерить штангенциркулем )

затем зная что масса вычисляется по формуле

m = pV

m = p¾πR³

опредеим массу

2) Положить шарик в мензурку ( имеющую деления шкалы ) с водой и измерить изменения объёма воды

Изменение объема воды будет равняться объему шарика .

Затем подвесить шарик на пружину с заранее известной жесткостью ( и определить максимальное удлинение пружины )

Итак как система неподвижна , тогда

Ox : kx - mg = 0

kx = mg

m = ( kx ) / g

По закону сохранения импульса

К примеру между двумя неупругими шарами ( двигающихся в направление друг друга ) происходит абсолютно неупругое центральное соударение

по закону сохранения импульса можем выразить ( массау одного из шаров мы знаем , и скорости их до соударения были равные ( однако m(1) > m(2) ) ( надо определить массу шара m(2) ) и общую скорость после соударения также знаем )

Оx : m(1)v - m(2)v = ( m(1) + m(2) )v'

m(1)v - m(2)v = m(1)v' + m(2)v'

- m(2)v - m(2)v' = m(1)v' - m(1)v

- m(2)( v + v' ) = m(1)( v' - v ) | * ( -1)

m(2)( v + v' ) = - m(1)( v' - v )

m(2) = ( - m(1)( v' - v ) ) / ( v + v' )

так и вычисляем по этой формуле

m(2) = - m(1) ( v' - v ) / ( v + v' )

4,6(88 оценок)

Ответ:

yanameleshko2016

27.04.2021

В задаче не указано, можно ли пользоваться таким понятием, как «момент инерции», поэтому мы обойдём этот вопрос при элементарного степенного интегрирования.

Итак. Нам требуется найти наибольшее значение силы давления стержня на ось $\overline{P}$ . По третьему закону Ньютона эта сила равна и противоположна силе давления оси на стержень в любой момент времени, а значит, мы, с таким же успехом, можем искать именно силу давления оси на стержень 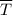$\overline{T}$ . Что мы и будем делать в решении.

Основные векторные построения и обозначения представлены на [рисунке 1]

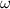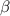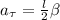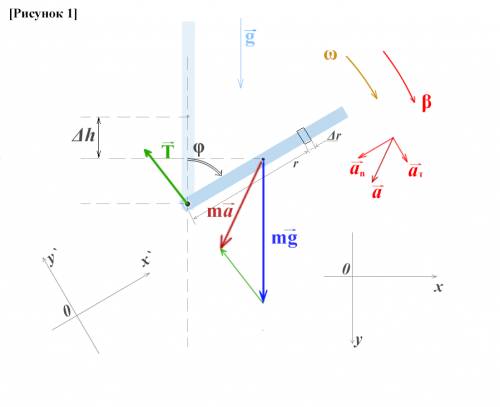
При прокручивании на оси, стержень приобретает угловую скорость $\omega$ , причём эта скорость нарастает, а значит, имеется угловое ускорение $\beta$ , у которого есть простая кинематическая связь c тангенциальным ускорением $a_\tau = \frac{l}{2} \beta$ центра масс стержня, расположенного в его середине. Здесь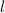

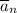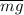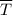– длина стержня. Помимо тангенциального ускорения у стержня есть и нормальное ускорение $\overline{a}_n$ , направленное вдоль него к оси. Это нормальное ускорение создаётся центростремительной силой, необходимой для удержания стержня, т.е. суммой продольных к стержню составляющих сил тяжести $\overline{mg}$ и давления оси на стержень $\overline{T}$ .

Как легко понять из рисунка:

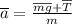$\overline{a} = \frac{ \overline{mg} + \overline{T} }{m}$ ;

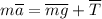$m \overline{a} = \overline{mg} + \overline{T}$ ;

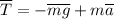$\overline{T} = -\overline{mg} + m \overline{a}$ : : : формула [1]

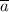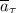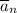Теперь найдём ускорение $\overline{a}$ , а для этого найдём его поперечную и продольную к стержню составляющие $\overline{a}_\tau$ и $\overline{a}_n$ :

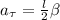$a_\tau = \frac{l}{2} \beta$ : : : формула [2]

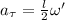$a_\tau = \frac{l}{2} \omega'$ ;

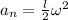$a_n = \frac{l}{2} \omega^2$ : : : формула [3]

Теперь, как мы видим, нам необходимо найти угловую скорость. Найдём её из закона сохранения энергии.

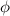Потенциальная энергия, при прокручивании стержня на угол $\phi$ убывает на 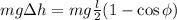$mg \Delta h = mg \frac{l}{2} ( 1 - \cos{ \phi } )$ . Кинетическую энергию в данном случае вычислить не так просто, поскольку каждый элемент стержня движется со своей скоростью, зависящей от того, насколько этот элемент удалён от центра вращения, так что близкие к оси его элементы имеют низкую скорость и малую кинетическую энергию, а удалённые – большую скорость и кинетическую энергию.

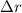Элемент, отмеченный на рисунке, как $\Delta r$ имеет массу 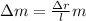$\Delta m = \frac{ \Delta r }{l} m$ и скорость 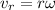$v_r = r \omega$ , значит, кинетическая энергия этого элемента: 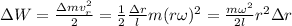$\Delta W = \frac{ \Delta m v_r^2 }{2} = \frac{1}{2} \frac{ \Delta r }{l} m ( r \omega )^2 = \frac{ m \omega^2 }{2l} r^2 \Delta r$ . Теперь для подсчёта всей кинетической энергии проинтегрируем эту элементарную кинетическую энергию по всей длине стержня:

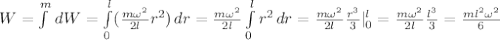$W = \int\limits^m \, dW = \int\limits^l_0 ( \frac{ m \omega^2 }{2l} r^2 ) \, dr = \frac{ m \omega^2 }{2l} \int\limits^l_0 r^2 \, dr = \frac{ m \omega^2 }{2l} \frac{r^3}{3} |_0^l = \frac{ m \omega^2 }{2l} \frac{l^3}{3} = \frac{ m l^2 \omega^2 }{6}$ ;

По закону сохранения энергии, убыль потенциальной энергии должна быть равна кинетической:

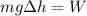$mg \Delta h = W$ ;

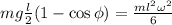$mg \frac{l}{2} ( 1 - \cos{ \phi } ) = \frac{ m l^2 \omega^2 }{6}$ ;

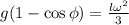$g ( 1 - \cos{ \phi } ) = \frac{ l \omega^2 }{3}$ ;

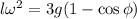$l \omega^2 = 3g ( 1 - \cos{ \phi } )$ : : : формула [4]

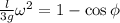$\frac{l}{3g} \omega^2 = 1 - \cos{ \phi }$ ;

Возьмём производную от этого уравнения:

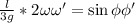$\frac{l}{3g} * 2 \omega \omega' = \sin{ \phi } \phi'$ ;

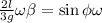$\frac{2l}{3g} \omega \beta = \sin{ \phi } \omega$ ;

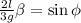$\frac{2l}{3g} \beta = \sin{ \phi }$ ;

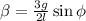$\beta = \frac{3g}{2l} \sin{ \phi }$ : : : формула [5]

Подставляя выражения [5] и [4] в формулы [2] и [3] получим

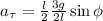$a_\tau = \frac{l}{2} \frac{3g}{2l} \sin{ \phi }$ ;

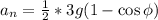$a_n = \frac{1}{2} * 3g ( 1 - \cos{ \phi } )$ ;

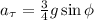$a_\tau = \frac{3}{4} g \sin{ \phi }$ : : : формула [6]

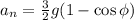$a_n = \frac{3}{2} g ( 1 - \cos{ \phi } )$ : : : формула [7]

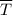Теперь осталась самая главная часть задачи. Поиск максимального значения силы давления оси на стержень $\overline{T}$ ;

К этому вопросу можно подойти на трёх уровнях сложности и, соответственно – достоверности.

Далее везде в основной неподвижной (лабораторной) системе отсчёта будем считать, что ось Ox направлена направо, а ось Oy направлена вниз, в ту же сторону, что и ускорение.

(продолжение решения на скришотах; формат сайта не позволил выложить более 5000 символов)

Однородный стержень массы m может свободно вращаться вокруг горизонтальной оси, проходящей через оди