 секунд от начала отсчёта времени – нос электрички уже был высунут за пределы моста на эти самые несколько десятков метров. Т.е. понятно, что нос электрички достиг окончания моста МЕНЕЕ ЧЕМ ЗА
секунд от начала отсчёта времени – нос электрички уже был высунут за пределы моста на эти самые несколько десятков метров. Т.е. понятно, что нос электрички достиг окончания моста МЕНЕЕ ЧЕМ ЗА 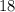 секунд!
секунд!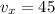 км/ч .
км/ч .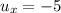 км/ч .
км/ч .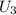 равна алгебраической сумме проекций
равна алгебраической сумме проекций 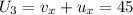 км/ч
км/ч 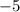 км/ч
км/ч 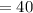 км/ч .
км/ч . секунд
секунд 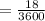 часа
часа 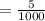 часа
часа 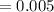 часа, студент относительно земли переместился точно на длину моста. Найдём длину моста
часа, студент относительно земли переместился точно на длину моста. Найдём длину моста 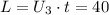 км/час
км/час 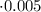 часа
часа 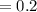 км
км 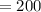 м .
м .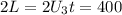 м .
м .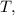 в течение которого ВСЯ электричка проезжала по мосту, разделим путь, который она проделала за это время на её скорость:
в течение которого ВСЯ электричка проезжала по мосту, разделим путь, который она проделала за это время на её скорость: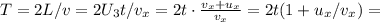
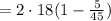 сек
сек 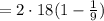 сек
сек 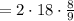 сек
сек 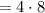 сек
сек 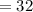 сек .
сек .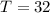 сек .
сек .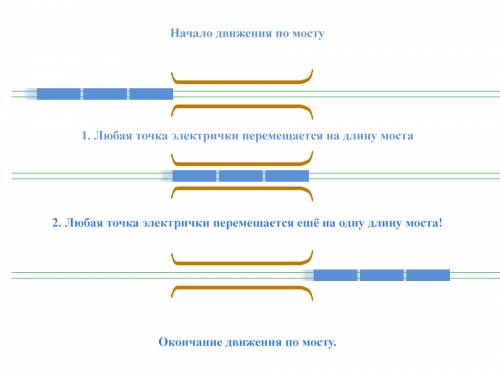
1) сделаем оценку энергии пули
Eк=m*V^2/2=0,015*320^2/2=768 Дж
2) найдем тепло на нагревание пули
Q1=c1*m*(0-t1)=2100*0,015*1=31.5 Дж
3) найдем тепло на плавление пули
Q2=л*m=3,4*10^5*0,015=5100 Дж
ясно что кинетической энергии пули не хватит чтобы лед нагрелся до 0 и расплавился
4) найдем тепло которое может отдать вода
Q3=c*M*(t1-0)=4200*2*1=8400 Дж
значит тепла воды хватит чтобы расплавить и разогреть лед
c*M*(t1-t)+Eк=с2*m*(0-t2)+л*m+c*m*t
t*c*(m+M)=Q3+Eк-Q1-Q2
t=(8400+768-31,5-5100)/4200*2.015=4036.5/4200*2,015=0.477С
ответ t~0,5C