Радиус малого поршня гидравлической машины – 1 мм. Большего поршня – 2 мм. На первый поршень давят с силой 100 Н, найдите силу с которой действует второй поршень.
2. Используя объём канистры, предполагая, что бензин занимает его полностью, и найдя плотность бензина в таблице плотностей: кг/м³, можем найти массу бензина:
3. Общая масса бензина с канистрой:
4. Вес, в данной задаче равный силе тяжести, находим по формуле: где м/с² - ускорение свободного падения.
5. Объединяем всё вышенаписанное в одну формулу:
Численно получим:
(Н).
ответ: 291 Н.→ Задача #2Дано:
Жёсткость пружины: Н/м.
Удлинение пружины: см = м.
Найти нужно массу груза:
Решение:
0. Сделаем небольшой рисунок, чтобы увидеть, как и какие силы действуют на груз.
1. Распишем второй закон Ньютона для данного рисунка: где м/с² - ускорение свободного падения.
2. В проекции на ось Оу (1) перепишется так:
3. Вспоминаем классическую формулу для силы упругости:
Абсолютная температура T = t + 273 T - температура кельвина t - температура по цельсию
Температура фаренгейта F = 32 + 1.8 C F - температура фаренгейта C - температура по цельсию
Количество тепла (теплоты) Q = cm(T_2 - T_1) Q - количество тепла c - удельная теплота m - масса T_1 - начальная температура T_2 - конечная температура
Горение топлива Q = qm Q - количество тепла q - удельная теплота сгорания m - масса
Теплота плавления Q = λ m Q - количество тепла λ - удельная теплота плавления m - масса
Испарение и количество тепла Q = L m Q - количество тепла L - удельная теплота испарения m - масса
Длина: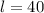
см = 
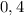м.
Высота: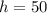
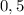см = 
м.
Ширина: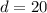
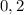см = 
м.
Масса канистры: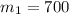
г = 
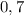кг.
Найти нужно общий вес бензина и канистры:
Решение:1. Найдём объём канистры: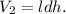
2. Используя объём канистры, предполагая, что бензин занимает его полностью, и найдя плотность бензина в таблице плотностей: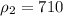
кг/м³, можем найти массу бензина: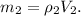 
3. Общая масса бензина с канистрой: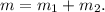
4. Вес, в данной задаче равный силе тяжести, находим по формуле: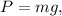
где 
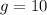м/с² - ускорение свободного падения.
5. Объединяем всё вышенаписанное в одну формулу: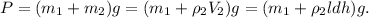
Численно получим:
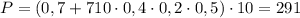(Н).
ответ: 291 Н.→ Задача #2Дано:Жёсткость пружины: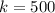
Н/м.
Удлинение пружины: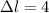
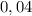см = 
м.
Найти нужно массу груза:
Решение:0. Сделаем небольшой рисунок, чтобы увидеть, как и какие силы действуют на груз.
1. Распишем второй закон Ньютона для данного рисунка: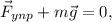
где 
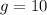м/с² - ускорение свободного падения.
2. В проекции на ось Оу (1) перепишется так: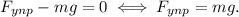
3. Вспоминаем классическую формулу для силы упругости: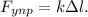
4. Объединяем (2) и (3):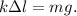
5. Выразим массу из (4):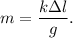
Численно получим:
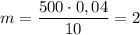(кг).
ответ: 2 кг.