Ядерные реакции классифицируются по виду бомбардирующих ядро частиц (альфа,бэта,гамма-излучения). Какая бомбардирующая частица применялась в следующих реакциях:
а) 7 N14 + ? = 8 О17 + 1 Н1?
б) 7 N14 + ? = 5 В11 + 2 Не4?
в)13A27+ 0 n1 = ? +2Не4
г) 25 Mn 55 +? = 26 Fe 55+ 0 n1
д) 3 Li 6 +1 H1 = 2Не4 + ?
е) 3 Li 7 + 2Не4 = 5 В
ответ: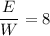
Объяснение:
Запишем уравнение гармонических колебаний в общем виде:
Будим считать, что маятник, в начальный момент времени, находился в положении максимального смещения от положения равновесия. В этом случае, когда мы отпустим маятник, он начнет совершать гармонические, незатухающие колебания.
Отсюда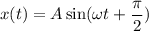
⇒ 
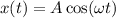(1)
Мы знаем, что потенциальную энергию пружинного маятника W, в любой момент времени t, можно вычислить как kx²(t)/2, а кинетическую энергию E, как mv²(t)/2.
То-есть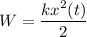
, но согласно уравнению (1) получим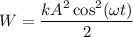 
Аналогично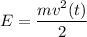
, однако мы знаем, что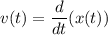 
Тогда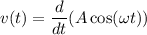
⇒ 
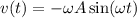, а это значит что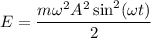 
Поэтому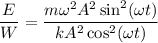
, так как 
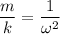, то 
⇒
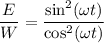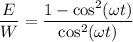(2)
Теперь определим cos²(ωt), мы знаем, что в нашем случае, в момент момент времени t растяжение пружины маятника составило А/3, тогда согласно уравнению (1)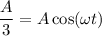
⇒ 
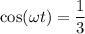, следовательно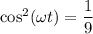 
Возвращаясь к уравнению (2) получим