Любые вращающиеся небесные объекты вращаются вокруг их общего центра тяжести. Например, Луна в 81 раз легче Земли, а расстояние между ними 380 000 км, это значит, что и Земля, и Луна вращаются вокруг некоторой точки, которая находится в пространстве на расстоянии L = 380 000 / 82 = 4600 км от центра Земли. Поскольку радиус земли равен 6370 км, то получается, что эта точка находится внутри Земли, значит скорее Луна вращается вокруг Земли, а Земля совершает некоторые эксцентрические колебания с той же частотой.
Решение: Частота - это число колебаний в единицу времени Частота колебаний математического маятника: Приравниваем две формулы: Откуда длина математического маятника: (вывод не буду удалять, может кому-то интересно будет ツ ) Длина первого маятника: Длина второго: Их соотношение: ───────────────────────────────────────────────── p.s ✎ Можно было в отдельно определить частоту колебаний первого маятника, затем второго и найти их соотношение. Также как вариант можно было через период решать
p=2575 кПа
ρ(моря) = 1030
g- 9,8
h-?
h=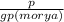
h=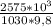 =254 метра
=254 метра
ответ: 254 метра
ps Не забудьте оценить мой ответ и показать насколько он был Вам полезен
Объяснение: