7. В один аквариум налили 2 л морской воды, в другой 4 л.
Уровень воды относительно дна в первом аквариуме ра:
вен 10 см, во втором — 20 см. В каком аквариуме давле-
ние на дно больше?
А. В первом в 2 раза больше
Б. во втором в 2 раза больше
В. давление одинаково

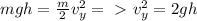
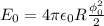
 :
: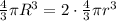
![r=\frac{R}{ \sqrt[3]{2} }](/tpl/images/0445/9339/75511.png)
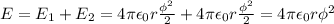
![\phi=\frac{1}{2}\frac{R}{r}\phi_0= \frac{ \sqrt[3]{2} }{2} \phi_0](/tpl/images/0445/9339/90628.png)
![E_k=\frac{m}{2}v_x^2=E_0-E=4\pi\epsilon_0 R\frac{\phi_0^2}{2}-4\pi\epsilon_0 r\phi^2=4\pi\epsilon_0(R\frac{\phi_0^2}{2}-\frac{R}{ \sqrt[3]{2} }\frac{ (\sqrt[3]{2})^2 }{4}\phi_0^2)](/tpl/images/0445/9339/43abf.png)
![E_0-E=4\pi\epsilon_0\phi_0^2R(\frac{1}{2}-\frac{\sqrt[3]{2}}{4})](/tpl/images/0445/9339/1cefd.png)
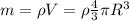 - суммарная масса двух частей, разумеется равна массе исходной капли.
- суммарная масса двух частей, разумеется равна массе исходной капли.![v_x^2=\frac{2}{\rho \frac{4}{3}\pi R^3}4\pi\epsilon_0\phi_0^2R(\frac{1}{2}-\frac{\sqrt[3]{2}}{4})=\frac{6}{\rho R^2}\epsilon_0\phi_0^2(\frac{1}{2}-\frac{\sqrt[3]{2}}{4})](/tpl/images/0445/9339/283d0.png)
![v_x^2=\frac{3\epsilon_0\phi_0^2}{\rho R^2}(1-\frac{\sqrt[3]{2}}{2})](/tpl/images/0445/9339/f743c.png)
![v= \sqrt{v_y^2+v_x^2} = \sqrt{2gh+\frac{3\epsilon_0\phi_0^2}{\rho R^2}(1-\frac{\sqrt[3]{2}}{2})}](/tpl/images/0445/9339/0d286.png)
1 вариант
1. P(тела в воде) = P(тела) - F(Архимеда)
P=mg - pgV
P=500kg*9.8m/c^2 - 1000kg/m^3*9.8m/c^2*0.2m^3= 5000H-2000H=3000H
2.
3. Плотность: парафина - ρ₁ = 900 кг/м³
дуба - ρ₂ = 700 кг/м³
пробки - ρ₃ = 240 кг/м³
При равном объеме шариков, выталкивающая сила, действующая на них, равна:
Fa = ρgV , где ρ - плотность жидкости.
Шарики находятся в равновесии (плавают в воде), поэтому их вес уравновешен выталкивающей силой.
Таким образом, на глубину погружения шариков в воду влияет только их вес: P₁ = m₁g = ρ₁Vg - парафин
P₂ = m₂g = ρ₂Vg - дуб
P₃ = m₃g = ρ₃Vg - пробка
Так как ρ₃ < ρ₂ < ρ₃, то: Р₃ < P₂ < P₁ => глубина погружения в воду из всех трех шариков будет максимальной у шарика из парафина, минимальной - у шарика из пробки.
ответ: на большую глубину погрузится шарик из парафина.
2 вариант
1. Объем вытесненной воды
V = 20*5*0,1 = 10 куб.м
Масса вытесненной воды
m = (po)* V = 1*10 = 10 тн
Вес вытесненной воды, равный весу трактора
P = m*g = 10*10^3 = 10000 H = 10 kH
2. на закрепе
3.парафин 900 кг/м³
дуб 690 кг/м³
пробка 240 кг/м³
Так как кубики одинакового объема, то уровень погружения напрямую зависит от плотности вещества, из которого изготовлен кубик. Из показаний плотности парафина, дуба и пробки можно сделать вывод, что на самую малую глубину погрузится кубик из пробки.