Объяснение:
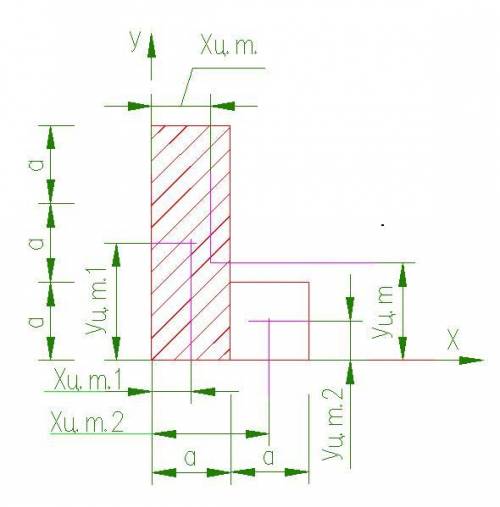
Пластина делится на две прямоугольные части.
У прямоугольника центр тяжести в середине.
У первой - заштрихованной пластины площадь 3a^2
А расстояния от координатных осей до центра тяжести:
Хцт1=0,5а
Уцт1=1,5а
У второй пластины площадь a^2
расстояния от координатных осей до центра тяжести:
Хцт2=1,5а
Уцт1=0,5а
Центр тяжести можно найти если просуммировать площади умноженные на расстояние до центра тяжести каждой простой фигуры, а потом эту сумму поделить на общую площадь.
Общая площадь фигуры 4а^2
Остается посчитать
Хц.т.=(3a^2*0,5а+a^2*1,5а)/4а^2=3а^3/4а^2=3а/4=0,75а
Уц.т.=(3a^2*1,5а+a^2*0,5а)/4а^2=3а^3/4а^2=5а/4=1,25а
Картинка приложена
3) 200
Объяснение:
Дано:
m = 1 кг
s(t) = 5t² - 2 (м)
t₁ = 2 c
Найти:
Ек₁ - кинетическую энергию тела через t c
В самом общем виде уравнение равноускоренного движения имеет вид
s(t) = s₀ + v₀t + 0.5 at²
По уравнению движения тела находим ускорение a
0.5at² = 5t²
0.5a = 5
а = 2 · 5 = 10 (м/с²)
Начальная скорость тела v₀ = 0, так как в уравнении движения
v₀t = 0
Скорость тела в момент времени t₁ = 2 c
v₁ = v₀ + at₁ = 0 + 10 · 2 = 20 (м/с)
Кинетическая энергия тела в момент времени t₁ = 2 c
Ек₁ = 0,5 mv₁² = 0.5 · 1 · 20² = 200 (Дж)