99 A
Объяснение:
U1=420B
I=297F
U2=140B
U1/I1=U2/I2
R1=R2=R
I2=I1*U2/U1
I2=297*140/420 = 99 A
Условие задачи:
Два тела масс m1 и m2, связанные невесомой нитью, лежат на гладкой горизонтальной поверхности. Нить обрывается, если сила её натяжения превышает значение Tm. C какой максимальной горизонтальной силой F можно тянуть второе тело, чтобы нить не оборвалась?
Задача №2.1.82 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
m1, m2, Tm, Fm−?
Решение задачи:
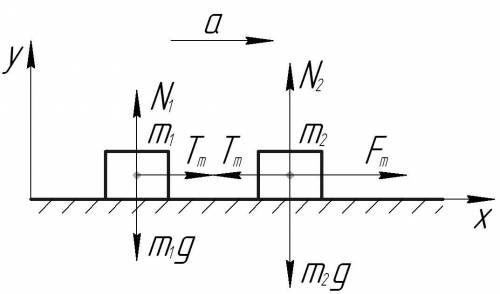
Схема к решению задачиПотянем второе тело с такой силой Fm, что сила натяжения нити, соединяющей тела, станет очень близка по величине к Tm, но ещё не разорвется.
По условию поверхность, по которой движутся тела, гладкая, значит сил трения нет. Покажем на схеме все силы, действующие на тела, потом запишем второй закон Ньютона для обоих тел в проекции на ось x. Ускорения рассматриваемых тел, естественно, одинаковые.
{Fm—Tm=m2aTm=m1a
Сложим оба выражения системы, а из полученного выразим ускорение a.
Fm=(m1+m2)a
a=Fmm1+m2
Подставим формулу в последнее выражение системы, а оттуда выразим искомую силу Fm.
Tm=Fmm1m1+m2
Fm=Tm(m1+m2)m1
Поделим почленно числитель дроби на знаменатель.
Fm=Tm(1+m2m1)
В условии не было дано числовых данных, задачу требовалось решить в общем виде, что мы и сделали.
ответ: Tm(1+m2m1)
Нахождение плотности тела, имеющего сложную геометрическую форму, по формуле (1) связано с определенными трудностями при выражении его объема через соответствующие линейные размеры. Метод гидростатического взвешивания обеспечивает возможность измерить объем этого тела, минуя использование масштабных линеек и нониусов.
Суть метода состоит в последовательном взвешивании данного тела в воздухе и в жидкости (воде) и нахождении по формуле Архимеда веса вытесненной телом (при его погружении) жидкости, а далее и самого объема погруженного в нее тела.
Во-первых, взвешивание тела, подвешенного к левой чашке весов на нити, в воздухе дает нам значение его массы с поправкой на архимедову силу в воздухе по формуле (6). Равновесие весов в этом случае описывается равенством:(*) (рис.2)
R= 420/297 = 140/99 = 1,41414
I2= 140 ÷ 140/99 = 140 × 99/140 = 99A.