На рисунке показаны графики зависимости от времени скоростей двух материальных точек, движущихся вдоль одной прямой от одного и того же начального положения.
Известно, что t1=3 с., а t2=19 с.
С точностью до десятых долей секунды определи, по истечении какого времени от момента начала наблюдения за точками они встретятся.
На рисунке показаны графики зависимости от времени скоростей двух материальных точек, движущихся вдоль одной прямой от одного и того же начального положения.
1 (1).svg
Известно, что t1=3 с., а t2=19 с.
С точностью до десятых долей секунды определи, по истечении какого времени от момента начала наблюдения за точками они встретятся.
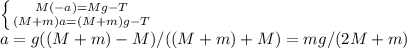
При движении по окружности возникает центростремительное ускорение, которое находится по формуле:
a = v²/R. Здесь v - линейная скорость вращения точки, а R - радиус окружности, который кстати сказать мы не знаем. Найдём его.
Линейная скорость вычисляется по формуле
v = ωR - где ω - угловая скорость вращения точки, а R - как раз нужный нам радиус.
Найдём теперь угловую скорость вращения. Это отношение угла поворота ко времени, за которое этот угол был пройден:
Точка по условию 1/6 * 2π = π/3 радиан.
Отсюда угловая скорость вращения:
ω = π/3 : 1 = π/3 радисан в секунду.
теперь мы знаем линейную и угловую скорость вращения, найдём отсюда радиус окружности:
R = v / ω = 10 / π/3 = 30/π = 10 м - это приблизительно.
Отсюда найдём ускорение:
a = 10 м/c²