Оба тела движутся равномерно.
х(t)=xo + Vx*t
x1=0 + 11,5 * t
x2=800 - 1 * t
Первое тело находится в начале отсчета. хо=0; его скорость 11,5 м/с вдоль оси координат.
Второе тело находится в точке с координатой 800 м и движется со скоростью (-1) м/с. Значит против оси координат, навстречу первому.
В начале наблюдения за телами (t=0) между телами было 800 м, но каждую секунду это расстояние уменьшается на (V1x - V2x)=
11,5 - (-1)=12,5 м/с
Тогда расстояние между ними S(t)=800 - 12,5*t
Это зависимость расстояния от времени. Цель задачи составить эту функцию. Теперь можно узнать расстояние между телами в любое время. И до встречи и после!
Через 10 с S(10)=800 - 12,5*10=800 - 125=675 м - это ответ.
Через минуту S(60)=800 - 12,5 * 60=50 м. Скоро встретятся. 50 м осталось.
Через 70 с S(70)=800 - 12,5 * 70=-75 м. Значит тела уже встретились и начинают удалятся друг от друга.
Дано:
T1= 1 секунда.
T2=1,1 cекунда.
a=?
_______
Из условия видно, что период увеличивается, следовательно лифт должен двигаться с ускорением, направленным вертикально вниз. (Данный факт следует из формул о весе тела, его движении вверх, или вниз с ускорением, так же, можно получить из второго закона Ньютона, расписывая силы, действущие на груз, который подвешен на математическом маятнике). ( длина маятника (l) - величина постоянная).
Запишем формулу периода математического маятника:
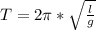
Теперь запишем данную формулу для двух случаев:
Возведем в квадрат и правую и левую часть каждого уравнения:
Поделим первое уравнение на второе:
Теперь выведем ускорение (а):
Посчитаем сначала периоды:
a=(g*(T2^2-T1^2)/(T1^2)=(g*(1,21-1)/(1,21)=0,17*g;
Подставляем значение ускорения свободного падения, равное, если быть более точным, 9,8 м/с^2.
a=0,17*9,8=1,666 м/с^2. Такое ускорение у лифтра. (если брать g=10м/с^2, то получим а=1,7 м/c^2).
ответ: а=1,666 м/с^2; (a=1,7 м/с^2).Лифт движется с ускорением, направленным вертикально вниз.