 секунд от начала отсчёта времени – нос электрички уже был высунут за пределы моста на эти самые несколько десятков метров. Т.е. понятно, что нос электрички достиг окончания моста МЕНЕЕ ЧЕМ ЗА
секунд от начала отсчёта времени – нос электрички уже был высунут за пределы моста на эти самые несколько десятков метров. Т.е. понятно, что нос электрички достиг окончания моста МЕНЕЕ ЧЕМ ЗА  секунд!
секунд! км/ч
км/ч  км/мин
км/мин  км/мин.
км/мин. км/ч
км/ч  км/мин.
км/мин.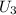 равна алгебраической сумме проекций
равна алгебраической сумме проекций 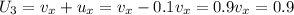 км/мин.
км/мин. секунд
секунд 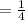 минут, студент относительно земли переместился точно на длину моста. Найдём длину моста
минут, студент относительно земли переместился точно на длину моста. Найдём длину моста  км/мин
км/мин  мин
мин 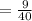 км
км  м
м  м .
м .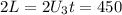 м .
м . в течение которого ВСЯ электричка проезжала по мосту, разделим путь, который она проделала за это время на её скорость:
в течение которого ВСЯ электричка проезжала по мосту, разделим путь, который она проделала за это время на её скорость:
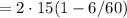 сек
сек 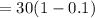 сек
сек  сек
сек  сек .
сек . сек .
сек .
 (1)
(1)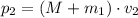 (2)
(2)
 (3)
(3) (4)
(4)
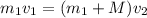
 (5)
(5)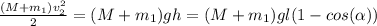
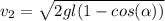 (6)
(6) (7)
(7)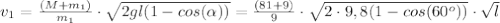
 м/с
м/с
ответ: 2130 Па
Объяснение:
На фото