Всё достаточно просто.
Формула, которая используется за основу для решения - обобщённая формула Бальмера. (фото 1)
В данной задаче рассматривают серию Лаймана (ультрафиолет), и это значит, что в формуле k= 1 - номер серии. (фото 2)
Как понятно из формулы( фото 2). Максимальная энергия будет при n₁ = 1 (const в формуле) и n₂=∞. Поэтому Emax = Ei = 0 - (-13,6) = 13,6 В
А минимальная энергия будет при n₁ = 1 (const в формуле) и n₂=2.
Emin = - 3,4 - (- 13,6) = 10,2 В
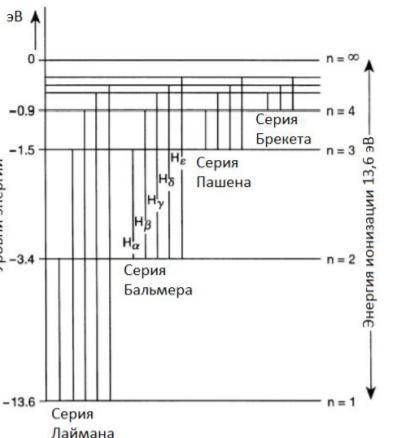
Значения берутся из серии (фото 3)
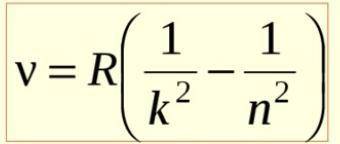
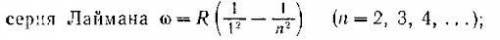
Fa=F₁-F₂, где Fa - сила Архимеда, F₁=20Н вес тела в воздухе, а F₂ =18,75Н вес тела в воде
Fa=ρ₀Vg, где ρ₀ = 1000 кг/м³ - плотность воды, V- объем короны, g=9,8 м/с² -ускорение свободного падения
отсюда получаем объем короны V=Fa/(ρ₀g)
F₁= ρVg, где ρ - плотность сплава короны
ρ=F₁/(Vg)=F₁/(gFa/(ρ₀g))=F₁/(Fa/ρ₀)=ρ₀F₁/Fa=ρ₀F₁/(F₁-F₂)=
=1000 кг/м³*20H/(20H-18,75H)=16000кг/м³
теперь найдем, сколько в короне было золота, а сколько серебра
Пусть m₁ и m₂ - массы золота и серебра в короне, а V₁ и V₂- объемы золота и серебра в короне
ρ₁ = 20000кг/м³ - плотность золота
ρ₂ = 10000кг/м³ - плотность серебра
тогда m₁=ρ₁V₁ и m₂=ρ₂V₂
(m₁ + m₂)g=F₁ или (ρ₁V₁+ ρ₂V₂)g=F₁
V₁+V₂=V
итак получаем систему из двух уравнений
(ρ₁V₁+ ρ₂V₂)g=F₁
V₁+V₂=V
c двумя неизвестными-V₁ и V₂
V₂=V-V₁
(ρ₁V₁+ ρ₂(V-V₁))g=F₁
ρ₁V₁+ ρ₂V-ρ₂V₁=F₁/g
ρ₁V₁-ρ₂V₁=F₁/g-ρ₂V
V₁(ρ₁-ρ₂)=F₁/g-ρ₂V
V₁=(F₁/g-ρ₂V)/(ρ₁-ρ₂)=(F₁/g-ρ₂Fa/(ρ₀g))/(ρ₁-ρ₂)=(F₁-ρ₂Fa/ρ₀)/g(ρ₁-ρ₂)
m₁=ρ₁V₁=ρ₁(F₁-ρ₂Fa/ρ₀)/g(ρ₁-ρ₂)=ρ₁(F₁-ρ₂Fa/ρ₀)/g(ρ₁-ρ₂)=
=20000кг/м³*(20H-10000кг/м³* (20H-18,75H)/1000кг/м³)/9,8 м/с²*(20000кг/м³-10000кг/м³)=20000кг/м³*(20H-10* 1,25H)/9,8 м/с²*10000кг/м³=2*(20H-10* 1,25H)/9,8 м/с²=1,53 кг
m₂=m-m₁=F₁/g-m₁=20H/9,8 м/с²-1,53 кг=0,511 кг
ответ: плотность короны 16000кг/м³, масса золота в ней 1,53 кг, а масса серебра 0,511