Отсюда мы видим, что график функции зависимости х от времени-парабола, которая ветвями направлена вниз. Отсюда, график пересекает ось ОХ в двух точках. Но в одной точке значение t будет отрицательное, поэтому этот корень отпадает, потому что время не может быть отрицательным. Теперь находим точку когда х=0:
Тело брошено вертикально вверх с начальной скоростью 20 м/с. Пренебрегая сопротивлением воздуха, определить, на какой высоте h кинетическая энергия тела будет равна его потенциальной энергии. Решение. В качестве нулевого уровня выберем уровень связанный с начальным положением тела. Потенциальная энергия тела в момент бросания равна нулю, так как потенциальная энергия является функцией высоты, кинетическая энергия равна mv2/2. В интересующей нас точке кинетическая энергия тела будет равна его потенциальной энергии (по условию задачи) Eк = Ep. (1) Запишем закон сохранения механической энергии (сопротивление среды отсутствует) mv2/2 = Eк + Ep = Ep + Ep = 2Ep. Здесь мы воспользовались (1) Тогда mv2/2 = 2mgh, или v2/(4g) = h После вычисления h = 202/(4 × 10) = 10 (м). ответ: на высоте 10 м кинетическая энергия тела равна его потенциальной.
1) x=-2t^2+4t+5
Отсюда мы видим, что график функции зависимости х от времени-парабола, которая ветвями направлена вниз. Отсюда, график пересекает ось ОХ в двух точках. Но в одной точке значение t будет отрицательное, поэтому этот корень отпадает, потому что время не может быть отрицательным. Теперь находим точку когда х=0:
0=2t^2-4t-5
D=16+40=56
x=0 t=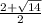
2) Дано- m=0.01кг, h=5м, t=1.2с
Найти - P-?
Решение
h=at^2/2 =>at^2=2h => a=2h/t^2 =>a=10/1.44=6.9 (м/с^2)
строим схему падения тела и получаем уравнение на ось ОУ:
ma=mg-N
N=mg-ma
N=P
P=mg-ma
P=0.01*10-0.01*6.9=0.1-0.069=0.031 (H)
ответ: 0.031 H