1.5 Обозначим скорость движения второго велосипедиста: v₂ км/ч,
скорость первого велосипедиста: v₁ км/ч,
скорость первого велосипедиста пешком: v км/ч.
По условию: v₁ = 4v
Тогда время движения первого велосипедиста:
t₁ = S₁/v₁ + S₂/v = 2/(4v) + 4/v (ч)
Время движения второго велосипедиста:
t₂ = (S₁+S₂)/v₂ (ч)
По условию: t₁ = t₂. Тогда:
2/(4v) + 4/v = 6/v₂
1/(2v) + 8/(2v) = 6/v₂
9v₂ = 12v = 3v₁ => v₁/v₂ = 9/3 = 3
ответ: Скорость езды первого велосипедиста больше, чем скорость второго в 3 раза.
1.6 Для более понятной записи обозначим расстояние, оставшееся после дождя до дома бабушки за S₃, а расчетную скорость движения за v.
Все расстояние обозначим S. Красная Шапочка (КШ) планировала пройти это расстояние со скоростью v за время t.
Вместо этого со скоростью v за время t₁ КШ только расстояние S₁ до начала дождя.
Затем какое-то время t₂, пока шел дождь, КШ двигалась со скоростью v₂, меньше расчетной, и расстояние S₂.
После этого оставшееся расстояние S₃ она со скоростью v₃, больше расчетной, за время t₃.
Так как S = S₁+S₂+S₃ и t = t₁+t₂+t₃, то:
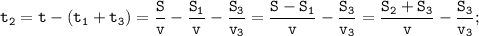
Напряжение на резисторах R₂ и R₁:
U₂ = U₁ = I₂R₂ = 2 · 2 = 4 (В)
Резисторы R₁ и R₂ соединены параллельно:
R₁₂ = R₁R₂/(R₁+R₂) = 1 · 2 : 3 = 2/3 (Ом)
Общая сила тока в цепи:
I = I₁₂ = I₃ = U₂/R₁₂ = 4 : 2/3 = 6 (A)
Общее сопротивление цепи:
R = R₁₂ + R₃ = 2/3 + 1 = 5/3 (Ом)
Напряжение на концах участка цепи (АВ):
U = I·R = 6 · 5/3 = 10 (B)
Если правый резистор, на самом деле не третий, а второй.
Тогда напряжение на нем:
U₂ = I₂R₂ = 2 · 2 = 4 (B)
Резисторы R₁ и R₃ соединены параллельно:
R₁₃ = R₁R₃/(R₁+R₃) = 1 · 1 : 2 = 0,5 (Ом)
Напряжение на группе R₁₃:
U₁₃ = I₁₃R₁₂ = 2 · 0,5 = 1 (В)
Напряжение на концах участка цепи (АВ):
U = U₁₃ + U₂ = 1 + 4 = 5 (B)