Расстояние между баржей и буксиром (S) = l, t =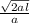 
, где а - ускорение баржи.
Объяснение:
1. Найдем на каком расстоянии будет баржа. Используем формулу без времени, тогда:
⇒ 
⇒ 
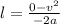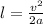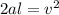, отсюда выражаем скорость:
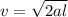. Найдем промежуток времени, который с момента открепления баржи от буксира до того момента, когда его скрость обращается в ноль.
По закону изменения модуля вектора скорости при равнопеременном движении:
, 
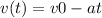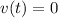, тогда можно записать:
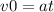, где 
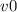- начальная скорость баржи, а следовательно и буксира.
Выражаем время:
⇒
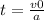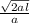
Δx =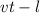 
, 
⇔ 
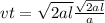, получаем:
Δx = 
= 
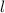= 1 км
0 для симметричной системы сил, если
радиан - в вашем случае скорее всего подразумевается этот простейший случай значит ответ 0
Объяснение:
Эта задача может показаться простой, только если угол между векторами равен 2π/N, решим ее для общего случая N одинаковых сил F, повернутых каждая относительно предыдущей на фиксированный угол α. Изобразим их на рисунке. Очевидно, что их суммарная проекция на ось х
на ось y
Результирующая сила будет равна
Исследуем получившуюся зависимость для разных N и α. Результаты показаны на графике.
Хорошо видно, что если α=0 то все силы просто складываются, а если α=2π/N, то мы получаем симметричную систему сил и равнодействующая равна нулю. Для нашего случая N=2021 имеем
В частности, если угол
то