Условие задачи:
Два тела масс m1 и m2, связанные невесомой нитью, лежат на гладкой горизонтальной поверхности. Нить обрывается, если сила её натяжения превышает значение Tm. C какой максимальной горизонтальной силой F можно тянуть второе тело, чтобы нить не оборвалась?
Задача №2.1.82 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
m1, m2, Tm, Fm−?
Решение задачи:
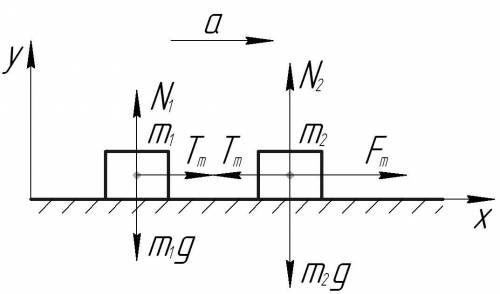
Схема к решению задачиПотянем второе тело с такой силой Fm, что сила натяжения нити, соединяющей тела, станет очень близка по величине к Tm, но ещё не разорвется.
По условию поверхность, по которой движутся тела, гладкая, значит сил трения нет. Покажем на схеме все силы, действующие на тела, потом запишем второй закон Ньютона для обоих тел в проекции на ось x. Ускорения рассматриваемых тел, естественно, одинаковые.
{Fm—Tm=m2aTm=m1a
Сложим оба выражения системы, а из полученного выразим ускорение a.
Fm=(m1+m2)a
a=Fmm1+m2
Подставим формулу в последнее выражение системы, а оттуда выразим искомую силу Fm.
Tm=Fmm1m1+m2
Fm=Tm(m1+m2)m1
Поделим почленно числитель дроби на знаменатель.
Fm=Tm(1+m2m1)
В условии не было дано числовых данных, задачу требовалось решить в общем виде, что мы и сделали.
ответ: Tm(1+m2m1)
Найти:
T = ?
Решение:
Согласно закону сохранения энергии: энергия никуда не исчезает, она лишь переходит из одного состояния в другое. В этой задаче такими состояниями/типами энергии являются - потенциальная и кинетическая составляющая, а также энергия потерь на сопротивление воздуху. Вся энергия постоянно перекачивается между этими тремя состояниями.
Изначально вся энергия шарика является потенциальной и равна
Когда шарик падает, он теряет потенциальную энергию, она переходит в кинетическую энергию и теряется на сопротивление воздуха. В конечный момент времени высота и вовсе равна нулю, а значит потенциальная энергия полностью перешла в энергию потерь и кинетическую и мы можем записать уравнение:
В левой части уравнения энергия в начале падения, а в правой - в конце падения.
Теперь можем найти кинетическую энергию шарика в момент удара о землю:
Получим численное значение
ответ: 36 Дж.