57,5 см
Объяснение:
Закон Архимеда:
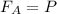, где сила Архимеда 
, ρ₁ - плотность воды, V₁ - объем погруженной части
тела, P - вес тела.
Для одной льдины закон Архимеда:
(1) 
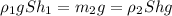, здесь ρ₁ - плотность воды, m₂ - масса льда, ρ₂ - плотность льда, S - площадь горизонального сечения льдины, h₁ - глубина погружения льдины в воду, h - высота льдины.
Отсюда: (2) 
см
Для льдины с медным кубиком:
(3) 
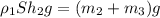, m₂ - масса льда, m₃ - масса медного кубика, h₂ - глубина погружения льдины в воду с установленным медным кубиком.
Подставляем сюда вместо m₂ выражение 1, получаем:
(4) 
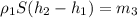, где h₂-h₁ =Δh
Теперь запишем закон Архимеда для льдины с железным кубиком:
, m₂ - масса льда, m₄ - масса железного кубика, H - глубина погружения льдины в воду с установленным железным кубиком.
Подставляем сюда выражение 1:
(5) 
.
Выразим массу железного кубика через массу медного:
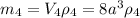, a - длина ребра куба, ρ₄ - плотность железа.
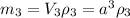, тогда:
(6) 
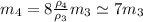
Подставляя (6), (4) в (5):
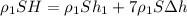
Упрощая это выражение и подставляя из (2) значение h₁:
см.
Небольшая ящерица - геккон - легко передвигается по гладким наклонных и вертикальных поверхностях, включая обычное стекло, а также ногами вверх по потолку, ведь пальцы гекконов имеют пластинки, на которых поперечными рядами располагаются особые щеточки с микроскопическими багатовершиннимы волосками (с электронного микроскопа было подсчитано, что на одном только пальцы геккона расположено более 200 000 000 таких щеточек, каждая из которых состоит из множества отдельных волосков). Благодаря своей ничтожно малой величине эти выросты охватывать самые мелкие неровности поверхности в сочетании с когтями позволяет ящерице легко передвигаться по гладким наклонных и вертикальных поверхностях.
Задача1.
Сначала напишем уравнение пути, пройденного автобусом за третью секунду движения:
S(3)=v0*t+(a*t^2)/2
Где S(3)- путь, пройденный за третью секунду,
v0 - начальная скорость, приобретённая автобусом за предшествующие две секунды движения, t - время рассматриваемого отрезка пути ( в данном случае оно равно1, ведь мы рассматриваем только путь, пройденный за одну, третью, секунду пути, а не за всё время) .
По условию задачи, путь, пройденный автобусом за третью секунду равен 3м:
S(3)=3
Получаем:
v0*t+(a*t^2)/2=3.
v0 в данном случае - это скорость, приобретённая за первую и вторую секунды движения. Она равна произведению ускорения на два (ведь с момента начала движения до начала третьей секунды две секунды) :
v0=2*a
Подставляя это равенство в исходное уравнение, имеем:
2*a*t+(a*t^2)/2=3.
Учитывая, что t=1 (см. выше) , получаем:
2*a+a/2=3
Выносим за скобку множитель a/2:
(a/2)*(4+1)=3
(a/2)*5=3
5*a=6
a=6/5=1,2м/с^2.
Итак, ускорение равно 1,2м/с^2.
Теперь, зная ускорение, найдём путь, пройденный автобусом за все 6 секунд, учитывая при этом, что вычисления будут отличны от расчёта пути за третью секунду из-за того, что начальная скорость в этом случае будет равна уже 0 - ведь вначале первой секунды автобус стоял:
S(6)=(a*t^2)/2= (1,2*6^2)/2= 1,2*36/2= 1,2*18= 21,6(м)
Теперь найдём путь, пройденный автобусом за 5 секунд:
S(5)=(a*t^2)/2= (1,2*5^2)/2= 1,2*25/2=0,6*25= 15(м)
Путь, пройденный за шестую секунду будет равен разности путей, пройденных за 6 и за 5 секунд:
S= S(6)-S(5)= 21,6-15=6,6(м)
Скорость вконце шестой секунды будет равна произведению ускорения на 6 секунд:
V(6)=a*t= 1,2*6= 7,2 м/с.
ответ S=6,6м. , a=1,2 м/с^2., V(6)=7,2М/с.
Задача2.
общий закон скорости при равноускоренном движении выглядит так:
Vx=V0+a*t
Нам же дана формула Vx =6t
Отсутствие первого слагаемого говорит о том, что V0=0
А множитель 6 есть ничто иное, как ускорение. Теперь напишем общий закон изменения координаты при равноускоренном дивжении:
x=x0+V0*t+(at^2)/2
При t=0, x тоже равен нулю ( по условию) :
x0=0
Так как V0=0(см. выше) , слагаемое V0*t так же обращается в ноль. Таким образом, уравнение приобретает вид:
x=0+0+(6t^2)/2. Окончательно, путём устранения нулей и вычислений в третьем слагаемом, получаем:
x=3t^2.
Это и есть искомое уравнение.
Искомый путь же вычисляется по уже не раз применённой нами формуле:
s=(a*t^2)/2=(6*10^2)/2= 6*100/2=300м.
ответ: S=300м., x=3t^2